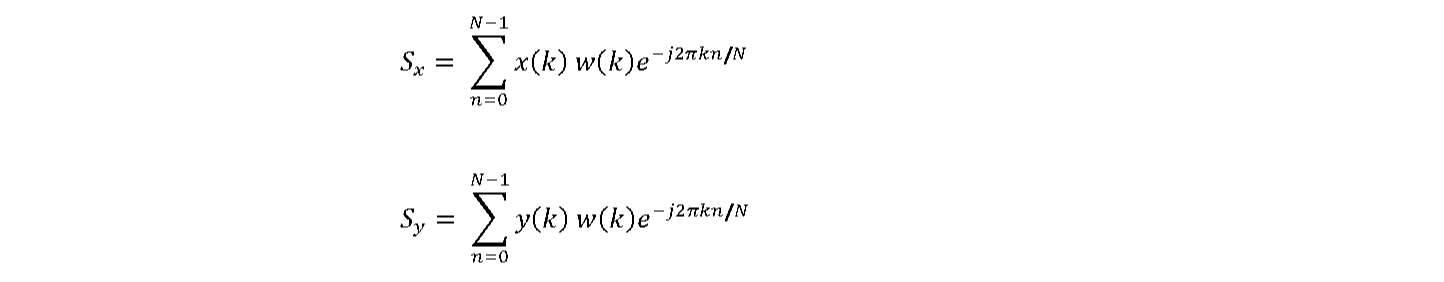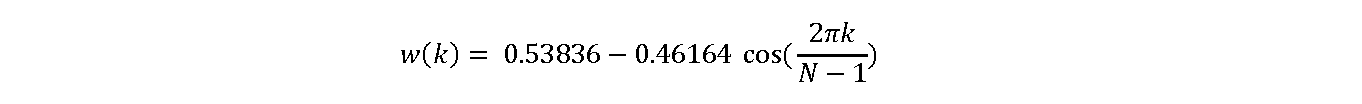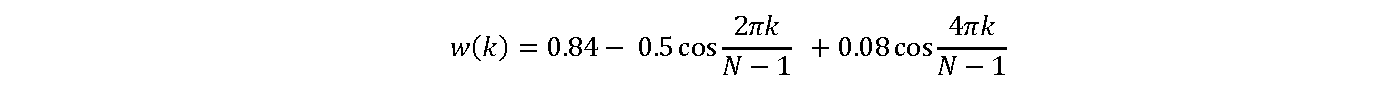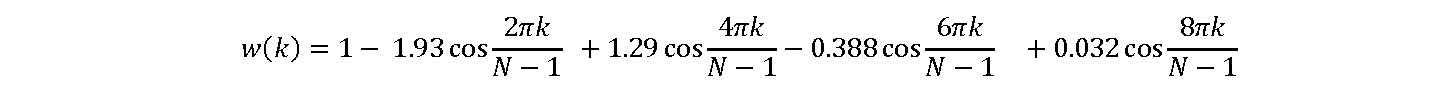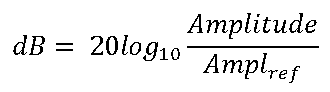Dynamic Signal Analysis Basics
Download PDF | James Zhuge, Ph.D. - Chief Executive Officer | Simran Parmar - Applications Engineer
© 2024 Crystal Instruments Corporation
Table of Contents:
1. Basic Theory of FFT Frequency Analysis | 2. Data Window Selection | 3. Averaging Techniques | 4. Transient Capture and Hammer Testing | 5. References
Basic Theory of FFT Frequency Analysis
DSA, often referred to Dynamic Signal Analysis or Dynamic Signal Analyzer depending on the context, is an application area of digital signal processing technology. Compared to general data acquisition and time domain analysis, DSA instruments and math tools focus more on the dynamic aspect of the signals such as frequency response, dynamic range, total harmonic distortion, phase match, amplitude flatness, etc. In recent years, time domain data acquisition devices and DSA instruments have gradually converged together. Progressively more time domain instruments, such as oscilloscopes, can perform frequency analysis and a growing number of dynamic signal analyzers can obtain long duration data recordings.
DSA uses various digital signal processing technologies. Among them, the most fundamental and popular technology is based on the Fast Fourier Transform (FFT). The FFT transforms the time domain signals into the frequency domain. Users need to understand the fundamental issues and computations involved to perform FFT-based measurements. This chapter describes some of the basic signal analysis computations, discusses anti-aliasing and acquisition front-end for FFT-based signal analysis, explains how to use windowing functions correctly, explains some spectrum computations, and demonstrates how to use FFT-based functions for some typical measurements.
This chapter will use standard notations for different signals. Each type of signal will be represented by one specific letter. For example, “G” represents a one-side power spectrum, while “H” represents a transfer function.
The following table defines the symbols used in this chapter:
| γyx | Coherence function between input signal x and output signal y |
| Gxx | Auto-spectral function (one-sided) of signal x |
| Gyx | Cross-spectral function (one-sided) between input signal x and output signal y |
| Hyx | Transfer function between input signal x and output signal y |
| k | Index of a discrete sample |
| Rxx | Auto-correlation function of signal x |
| Ryx | Cross-correlation function between input signal x and output signal y |
| Sx | Linear spectral function of signal x |
| Sxx | Instantaneous auto-spectral function (one-sided) of signal x |
| Syx | Instantaneous cross-spectral function (one-sided) between input signal x and output signal y |
| t | Time variable |
| x(t) | Time history record |
| X(f) | Fourier Transform of time history record |
Fourier Transform
Digital signal processing technology includes FFT based frequency analysis, digital filters, and many other topics. This chapter introduces the FFT based frequency analysis methods that are widely used in all dynamic signal analyzers. Crystal Instrument’s analyzers fully utilize the FFT frequency analysis methods and various real time digital filters to analyze the measurement signals.
The Fourier Transform is a transform used to convert quantities from the time domain to the frequency domain and vice versa, usually derived from the Fourier integral of a periodic function when the period grows without limit, often expressed as a Fourier transform pair. In the classical sense, a Fourier transform takes the form of:
∞
X(f) = ∫ x(t)e-j2πft dt
-∞
Where:
| x(t) | continuous time waveform |
|---|---|
| f | frequency variable |
| j | complex number |
| X(f) | Fourier transform of x(t) |
Mathematically the Fourier Transform is defined for all frequencies from negative to positive infinity. However, the spectrum is usually symmetric, and it is common to only consider the single-sided spectrum which is the spectrum from zero to positive infinity. For discrete sampled signals, this can be expressed as:
N−1
X(k) = ∑ x(n)e−𝑗2𝜋k/N
n=0
Where:
| x(n) | samples of time waveform |
|---|---|
| n | running sample index |
| N | total number of samples or “block size” |
| k | finite analysis frequency, corresponding to “FFT bin centers” |
| X(k) | discrete Fourier transform of x(k) |
In most DSA products, a Radix-2 DIF FFT algorithm is used, which requires that the total number of samples must be a power of 2 (total number of samples in FFT = 2m, where m is an integer).
Sampling Rate Selection
The most important parameter to consider before performing an FFT is the sampling rate. This dictates the highest frequency component that can be resolved. Before discussing sampling rate, it is important to understand the Nyquist-Shannon sampling theorem. It states that if a system uniformly samples an analog signal at a rate that exceeds the signal’s highest frequency component by a factor of at least 2 then the original analog signal can be recovered exactly from the discrete samples.
Nyquist Frequency = 2 ∙ Maximum Signal Frequency
This can be better understood with an illustration. Consider a 2 Hz sine tone.
Figure 1. 2 Hz sine function.
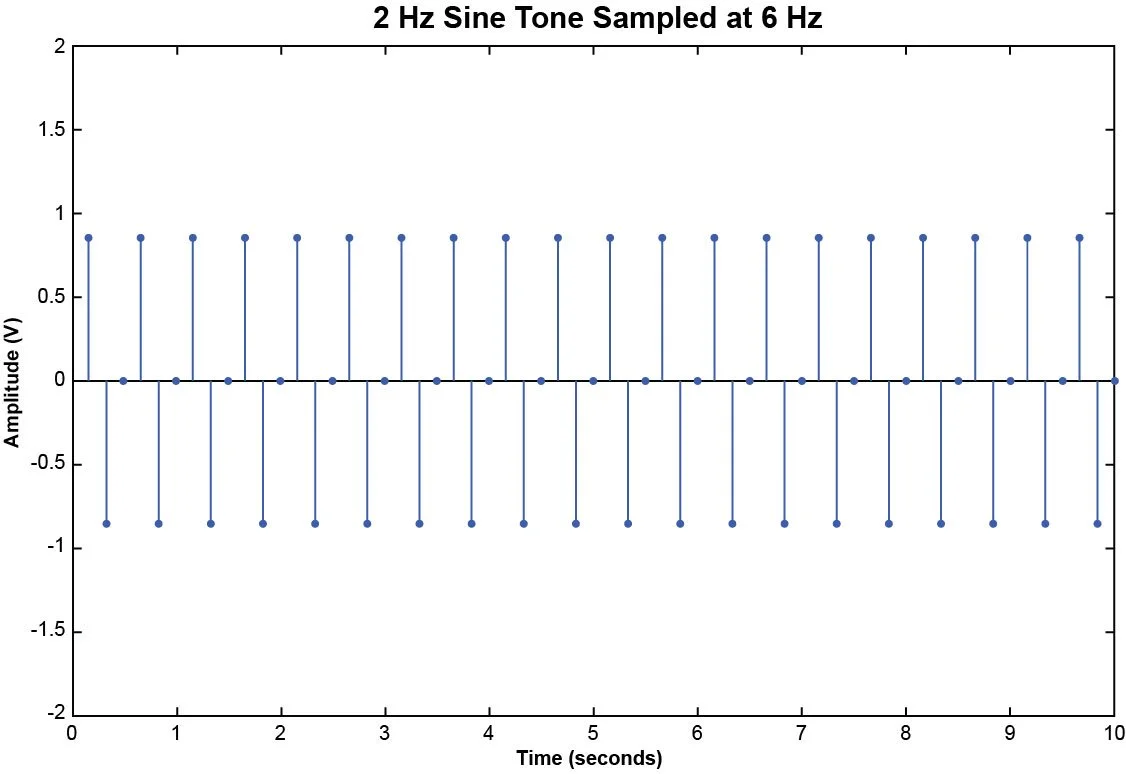
Now suppose we sample this 2 Hz sine tone with a sampling rate of 6 Hz. Then in a period of 10 seconds, we will have acquired 60 discrete samples.
Figure 2. Samples of a 2 Hz sine tone acquired at 6 samples per second.
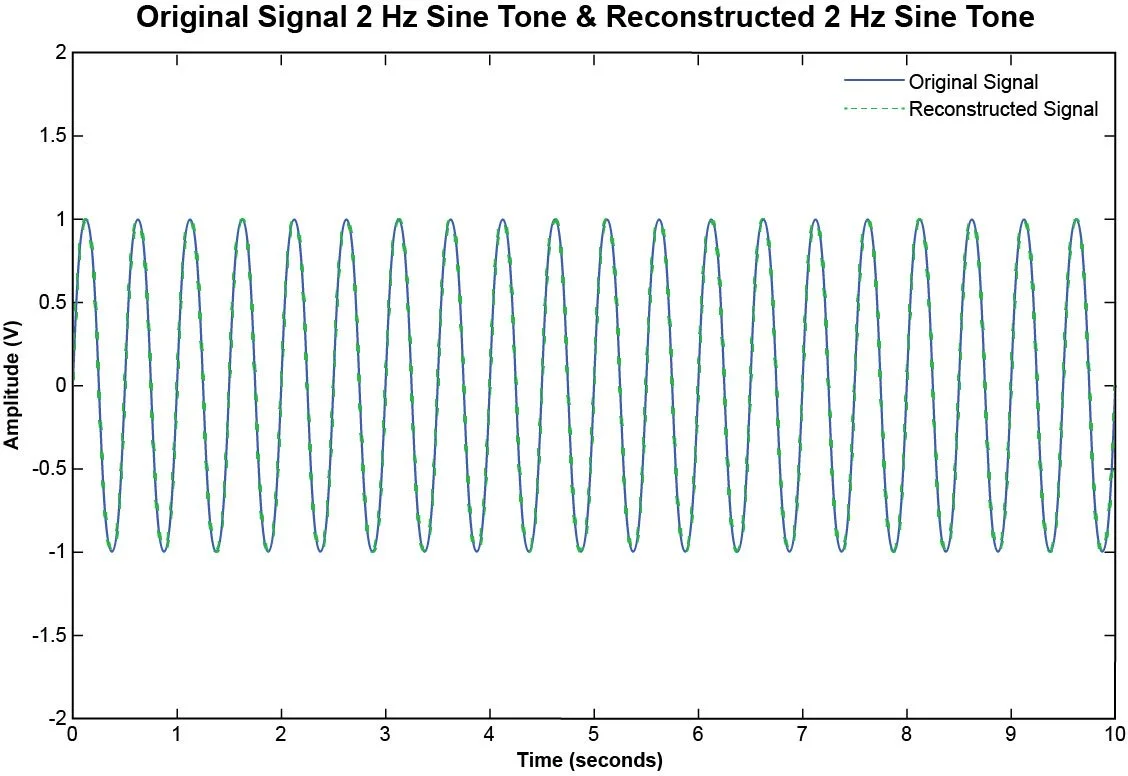
Since the sampling rate is greater than twice the frequency of the sine tone, we can reconstruct the analog signal via interpolation using the Sinc function.
∞
x(t) = ∑ x[n] ∙ sinc (t − nT / T)
n=−∞
where x[n] are the sampled values of x(t) and T is the sampling period
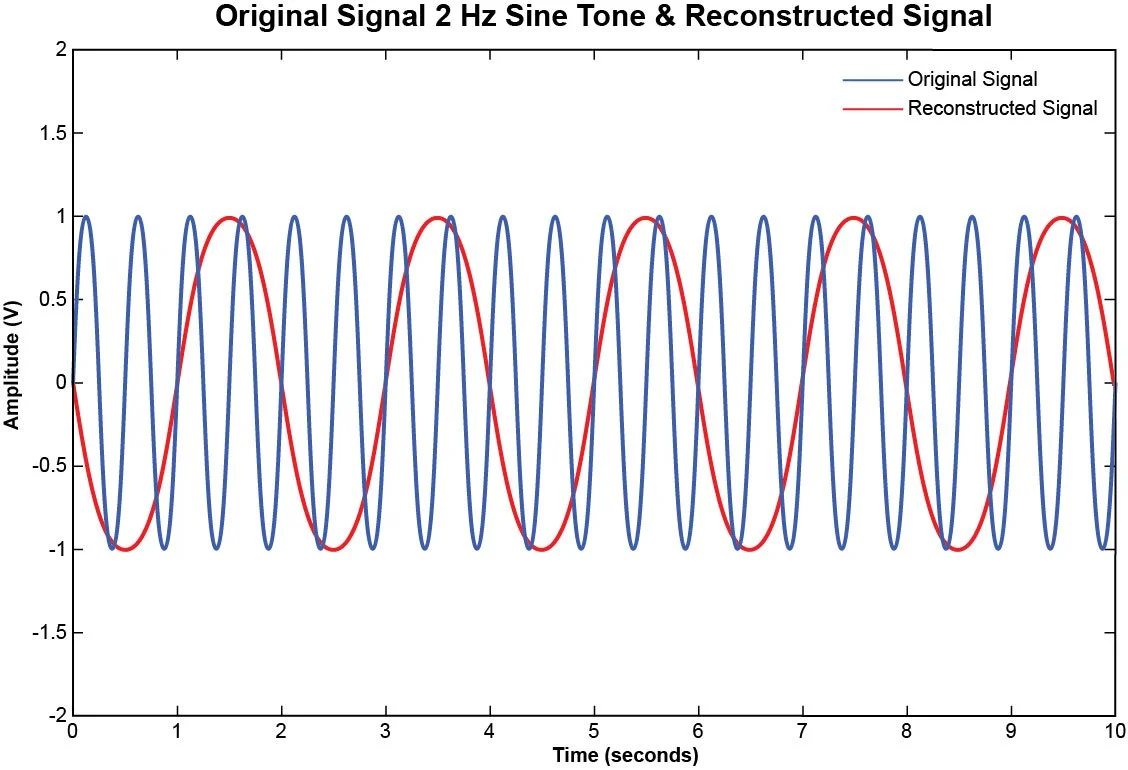
Figure 3. Continuous 2 Hz sine tone overlaid with a properly reconstructed 2 Hz sine tone.
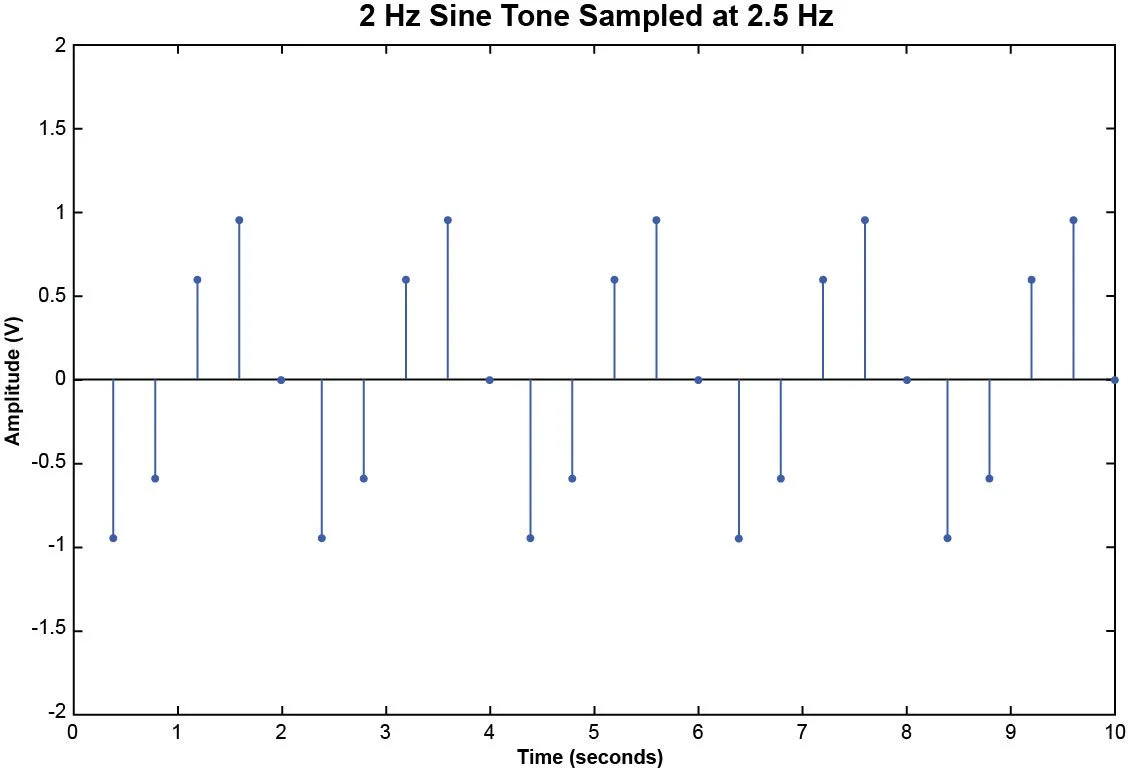
The reconstructed signal is almost identical to the original signal. Now suppose we sampled the 2 Hz sine tone with a sampling rate of 2.5 Hz instead of 6 Hz. In a period of 10 seconds, we will have acquired 25 samples.
Figure 4. Samples of a 2 Hz sine tone acquired at 2.5 samples per second.
The original 2 Hz sine wave cannot be reconstructed with the 25 samples from Figure 4. If an attempt is made, the resulting analog waveform will be an aliased signal.
From the plot in Figure 5, we can observe the reconstructed signal has a lower frequency than the original signal. This phenomenon is attributed to aliasing in the reconstructed signal, stemming from the fact that the samples utilized for its construction were acquired at a rate lower than the Nyquist frequency.
Figure 5. Continuous 2 Hz sine tone overlaid with an aliased sine tone.
Anti-Aliasing Filter
It is now established that a sampling rate exceeding the Nyquist frequency by a factor of 2 is essential for proper analysis. However, in many cases, the bandwidth of a given signal remains elusive and consequently the Nyquist frequency is unknown. To address this challenge, a signal should first be passed through an anti-aliasing filter before being sampled as illustrated in Figure 6. This filter serves to limit the upper threshold of the signal frequency, effectively preventing aliasing.
Figure 6. Block diagram depicting the anti-aliasing filter and the ADC.
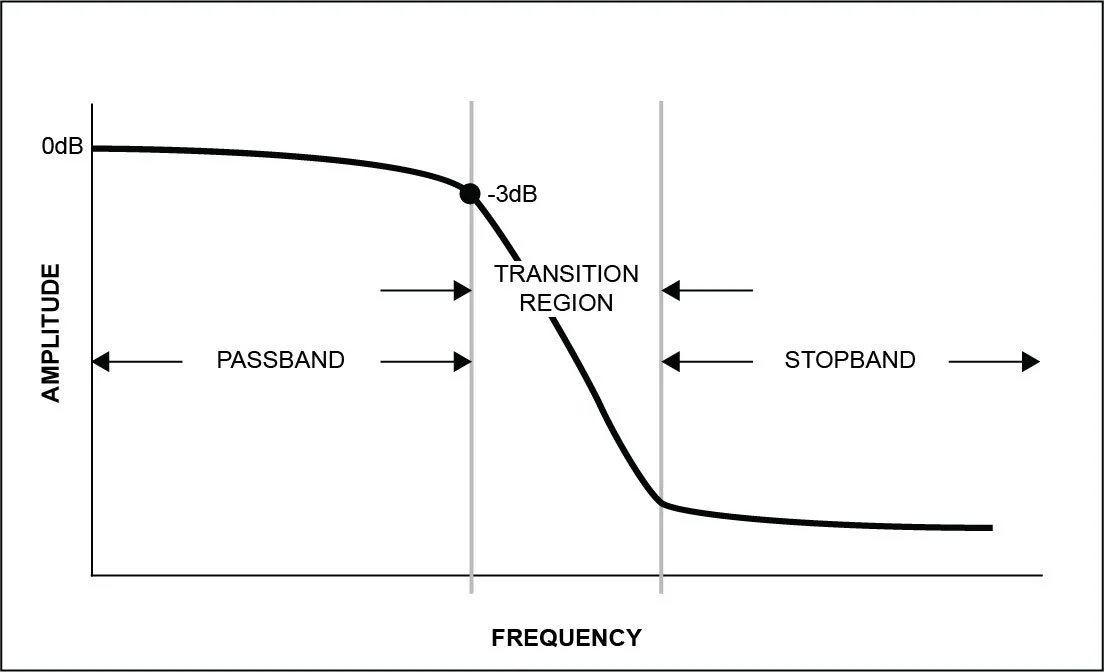
Crystal Instruments’ DAQs are equipped with anti-aliasing filters. The cut-off frequency of the filters varies based on the sampling rate of the system. Ideally, the cutoff frequency should be exactly half the sampling rate according to the Nyquist-Shannon sampling theorem. However, this would require a ‘brick wall’ filter, where all frequency components equal to or less than the Nyquist frequency are passed through without any attenuation and where all frequency components above the Nyquist frequency are attenuated completely. A real anti-aliasing filter will have a frequency response like the plot depicted in Figure 7.
Figure 7. Frequency response curve for a typical anti-aliasing filter.
The frequency response curve from the plot above can be separated into 3 sections:
Passband – frequency components in the passband are unattenuated by the filter.
Transition Region – frequency components are attenuated by at least 3 dB.
Stopband – frequency components are attenuated completely.
Crystal Instruments incorporates anti-aliasing filters with a transition region initiating at 0.45 times the sampling rate, and the cut-off frequency is adjusted accordingly.
Cut-off frequency = 0.45 ∙ Sampling Rate
This cut-off frequency assures users that the acquired data is uncontaminated by aliased signals. By integrating the anti-aliasing filter alongside an appropriately chosen sampling rate, it becomes possible to conduct an accurate spectral analysis.
Block Size
As mentioned earlier, the block size must conform to a power of 2 as required by the Fast Fourier Transform algorithm. In Crystal Instruments devices and EDM software, the block sizes are listed as two numbers:
Block Size: Time Domain Points / Spectral Lines
The Time Domain Points refer to the number of samples to be acquired prior to initiating any signal processing procedures. An alternative perspective is to link the time domain points with the duration of the captured data according to the following formula:
Duration = (Time Domain Points)/(Sampling Rate)
For example, with a sampling rate of 102.4 kHz and a block size of 1024/450, the duration of capture is calculated as follows:
1024/102400 Hz = 0.01 seconds
This means that each block consists of 0.01 seconds of data captured in the time domain. Thus, every second of an incoming time steam will be partitioned into 100 blocks.
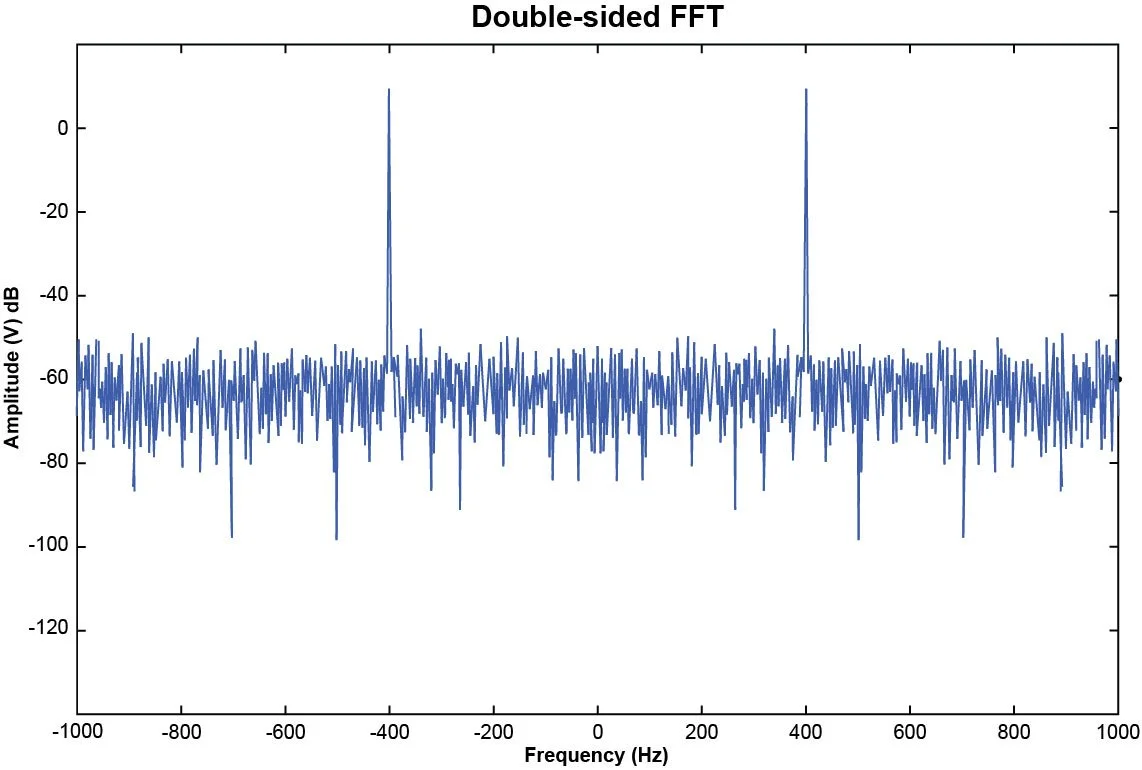
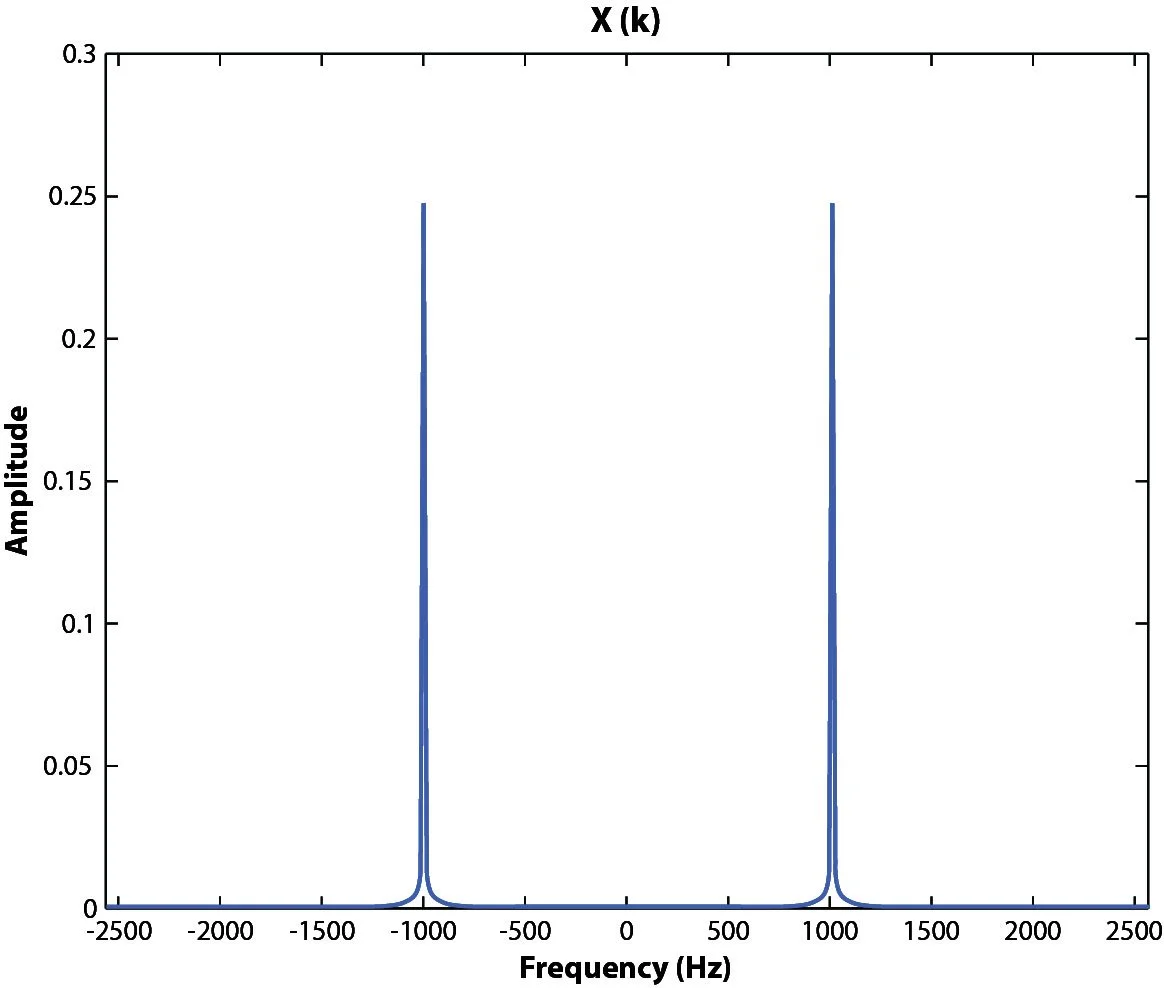
Spectral Lines refer to the number of frequency domain points produced after an FFT is applied to the set of time domain points. The FFT algorithm takes an input of N sample points and produces a frequency spectrum of N points. The spectrum produced ranges from the negative Nyquist frequency to the positive Nyquist frequency. The values associated with the negative frequencies are mirrored duplicates of the magnitudes associated with the positive frequencies, as illustrated in Figure 8.
Figure 8. Double-sided FFT of a 400 Hz sine tone.
Since the FFT spectrum is mirrored about 0 Hz, the magnitudes associated with the negative frequencies may be discarded and in theory the number of spectral lines can be exactly half the number of time domain points, N/2. However, as previously mentioned, the cut-off frequency is 0.45∙Samping Rate and so some of the spectral lines that would have appeared near the end of the Nyquist frequency are omitted. The number of spectral lines and time domain points are associated as:
Spectral Lines ~ 0.44 ∙Time Domain Points
Consider a spectrum produced using data sampled at 1 kHz and a block size of 1024/450. Then 512 spectral points could be used to represent the frequency response up to the Nyquist rate of 500 Hz. Instead of 512 spectral points, 450 will be used to represent the frequency range up to 439 Hz.
Now, spectral analysis is performed on a block-by-block basis, meaning each block of data is independently transferred to the frequency domain via the FFT algorithm. Furthermore, the frequency resolution of the spectrum produced is entirely determined by the sampling rate and block size as specified by the following equation:
∆f = (Frequency Range)/(Spectral Lines)
Building upon the preceding example, the frequency resolution of the spectrums produced with a sampling rate of 102.4 kHz and a block size of 1024/450 is calculated as follows:
∆f = 46080 Hz/450 = 102.4 Hz
This implies that within the frequency range spanning 0 Hz – 46080 Hz, 450 spectral lines will emerge, starting at 102.4 Hz and ending at 46080 Hz, each spaced uniformly by 102.4 Hz.
Frequency resolution becomes critical when analyzing signals that may encompass dominant frequency components positioned in close proximity to each other.
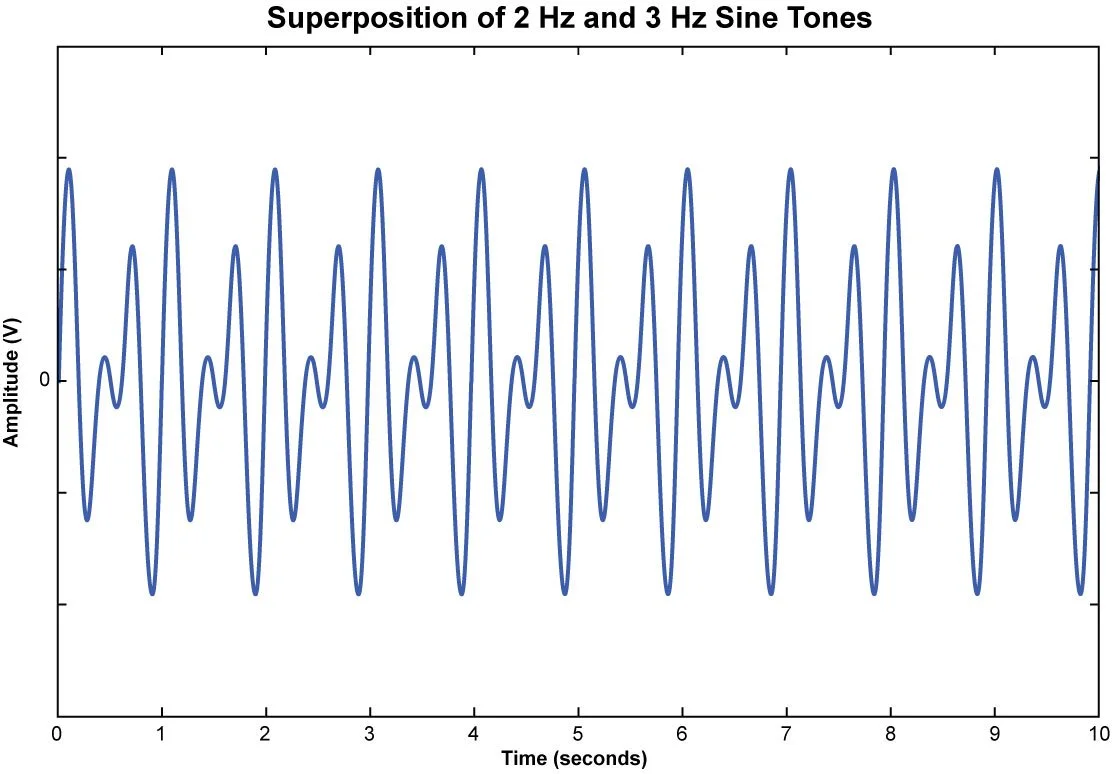
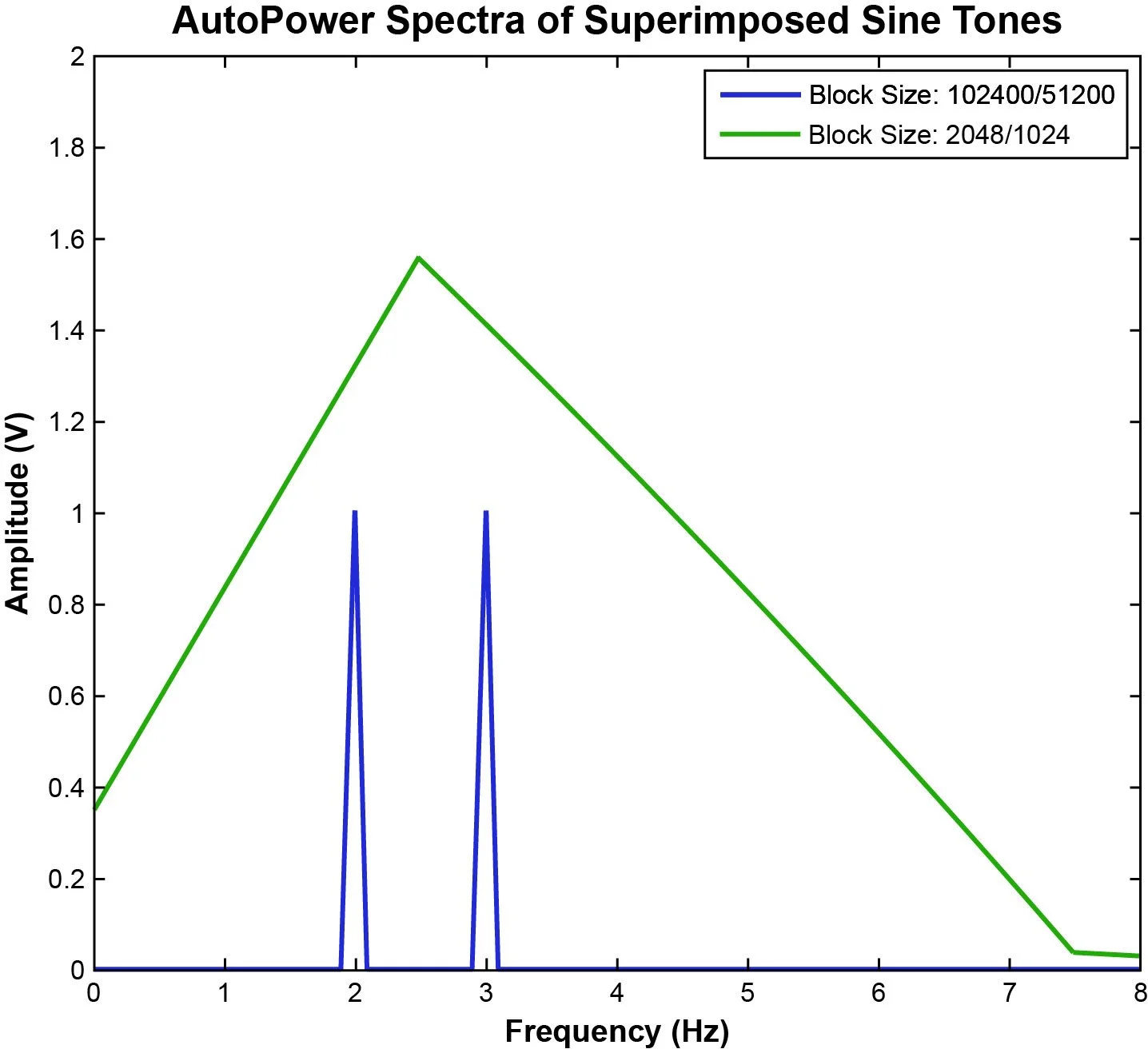
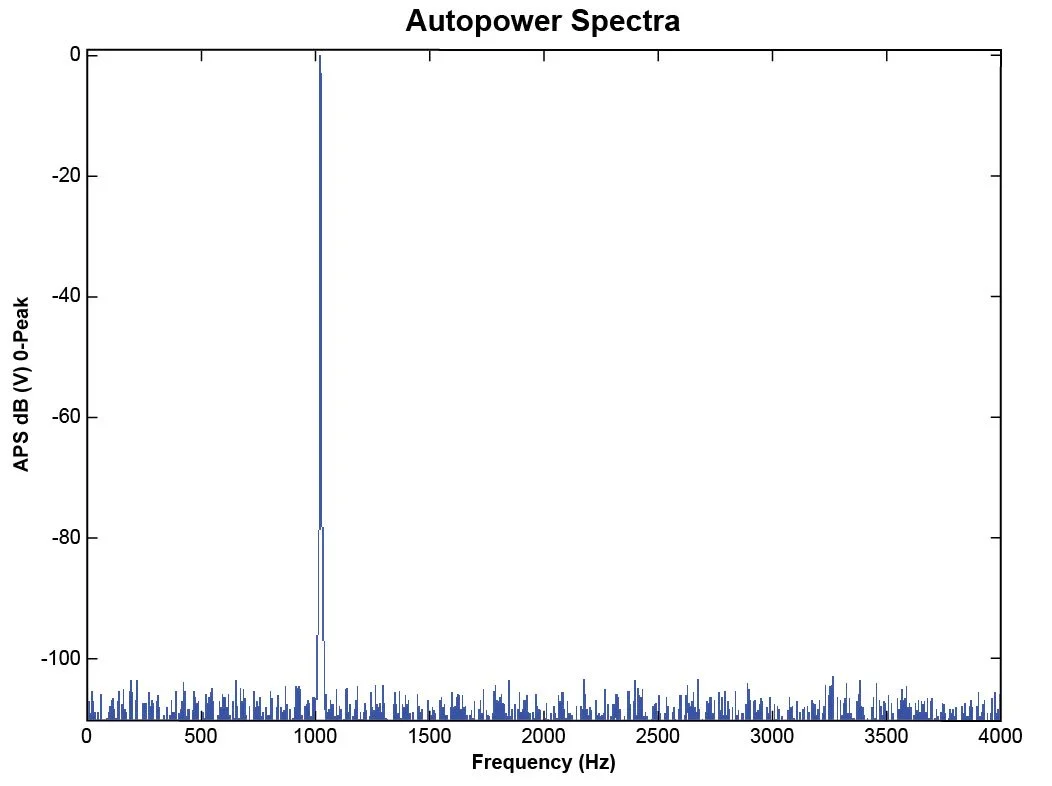
Suppose an incoming signal sampled at 5120 Hz is comprised of a superposition of two sine tones, one with a frequency of 2 Hz and the other with a frequency of 3 Hz. (Figure 9)
Figure 9. Superposition of sine tones as a function of time.
The two tones are spaced 1 Hz apart and so to determine the magnitude of contribution from each tone on the complete signal requires careful block size selection. Suppose a block size of 102400/51200 is used to produce the AutoPower Spectra. With a sampling rate of 5120 Hz and 51200 spectral lines, the frequency resolution is as follows:
∆f = 2560 Hz/51200 = 0.05 Hz
Similarly, with a block size of 2048/1024 the resulting frequency resolution is:
∆f = 2560 Hz/1024 = 2.5 Hz
Figure 10 displays both APS spectrums: a blue spectrum with a block size of 102400 and a green spectrum with a block size of 2048. However, only the blue spectrum provides a high enough frequency resolution to resolve the dominant 2 Hz and 3 Hz tones.
Figure 10. APS of a superposition of sine tones with a frequency bin width of 0.05 Hz.
The green spectrum, produced with a frequency resolution of 2.5 Hz, does not distinguish the 2 Hz and 3 Hz tones as they are only 1 Hz apart. Part of the contribution of the 2 Hz tone is placed in the 0 Hz – 2.5 Hz bin, part of the contributions from the 2 Hz and 3 Hz tones are placed in the 2.5 Hz – 5 Hz bin, and part of the contribution of 3 Hz tone is placed in the 5 Hz – 7.5 Hz bin.
The key insight here is the necessity to select an appropriate block size that provides a sufficient frequency resolution to distinguish dominant frequencies.
Data Windowing
The Fourier Transform assumes that the time signal is periodic and infinite in duration. When only a portion of a record is analyzed, the block must be truncated by a data window to preserve the frequency characteristics. A window can be expressed in either the time domain or in the frequency domain, although the former is more common. To reduce the edge effects, which cause leakage, a window is often given a shape or weighting function. For example, a window can be defined as:
w(t) = g(t) , T/2 < t < T/2
= 0 elsewhere
where g(t) is the window weighting function and T is the window duration.
The data analyzed, x(t) are then given by
x(t) = w(t)x(t)'
where x(t)' is the original data and x(t) is the data used for spectral analysis.
A window in the time domain is represented by a multiplication and hence, is a convolution in the frequency domain. A convolution can be thought of as a smoothing function. This smoothing can be represented by an effective filter shape of the window, i.e., energy at a frequency in the original data will appear at other frequencies as given by the filter shape. Since time domain windows can be represented as a filter in the frequency domain, the time domain windowing can be accomplished directly in the frequency domain.
In most DSA products, rectangular, Hann, Flattop and several other data windows are used.
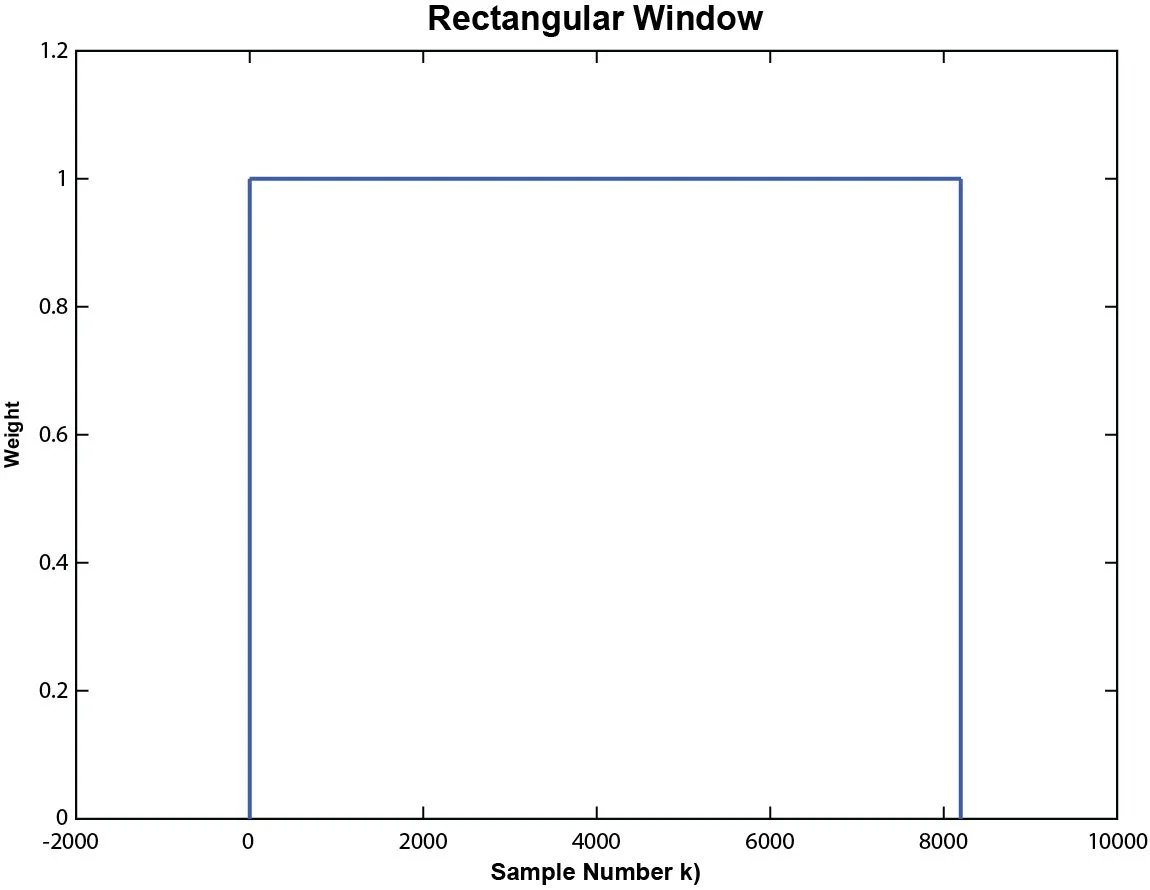
Rectangular Window
w(k)=1
0 ≤ k ≤ N-1
Figure 11. Rectangular window with a block size of 8192.
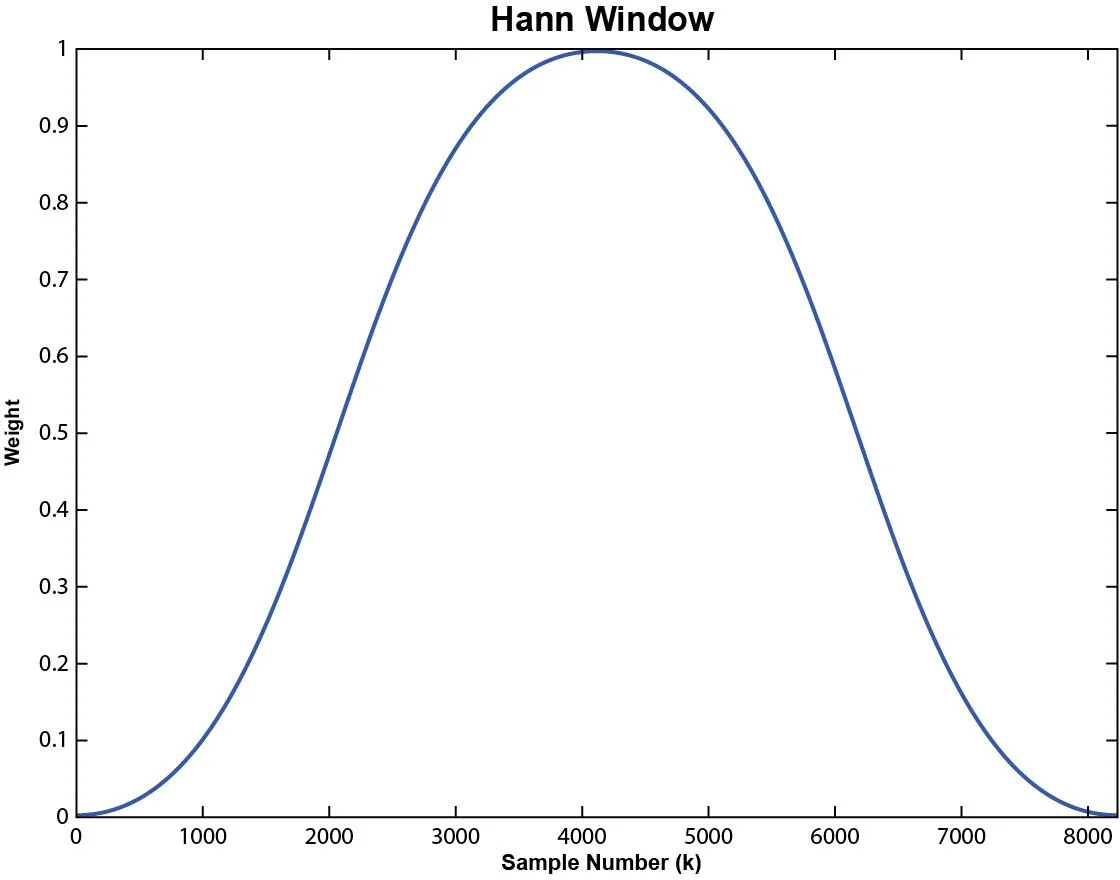
Hann Window
0 ≤ k ≤ N-1
Figure 12. Hann Window with a Block Size of 8192.
Since creating a data window attenuates a portion of the original data, a certain amount of correction is required to obtain an un-biased estimation of the spectra. In linear spectral analysis, an Amplitude Correction is applied; in power spectral measurements, an Energy Correction is applied. Refer to the following sections for details.
Linear Spectrum
A linear spectrum is the Fourier transform of windowed time domain data. The linear spectrum is useful for analyzing periodic signals. Users can extract the harmonic amplitude by reading the amplitude values at those harmonic frequencies.
An averaging technique is often used in the time domain when synchronized triggering is applied. Or equivalently, the averaging can be applied to the complex FFT spectra.
Because the averaging is taking place in the linear spectrum domain, or equivalently, in the time domain, based on the principles of linear transform, averaging does not make sense unless a synchronized trigger is used.
Most DSA products use the following steps to compute a linear spectrum:
Step 1
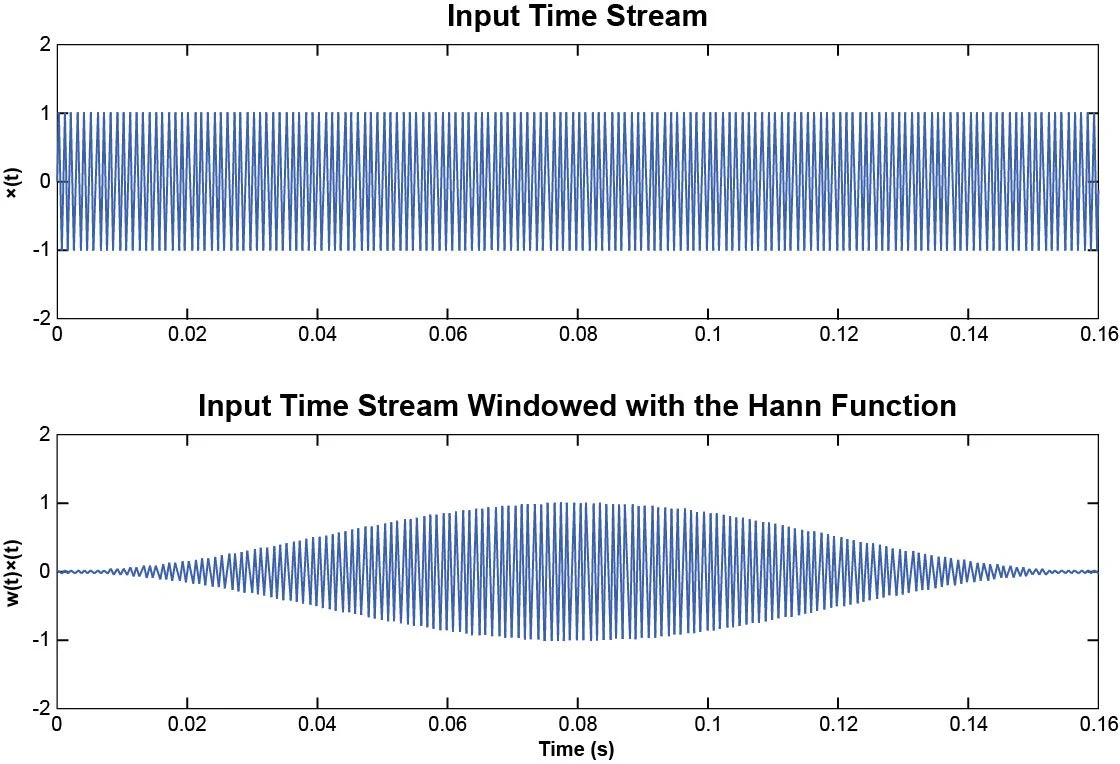
First a window is applied:
x(t) = w(t)x(t)'
where x(t)' is the original data and x(t) is the data used for the Fourier transform. (Example: Figure 13)
Figure 13. Plot of the original signal and its windowed version.
Step 2
The FFT is applied to x(t) to compute X(k), as described above. (Example: Figure 14)
Figure 14. Double-sided FFT
Step 3
Averaging is applied to X(k). Here averaging can be either an Exponential Average or Stable Average. Result is Sx'.
S'x = Average (X(k))
Step 4
To obtain a single-sided spectrum, double the value for symmetry about DC.
An Amplitude Correction factor is applied to S'x so that the final result has an un-biased reading at the harmonic frequencies.
Sx = (2S'x)/AmpCorr
where AmpCorr is the amplitude correction factor, defined as:
where w(k) is the window weighting function.
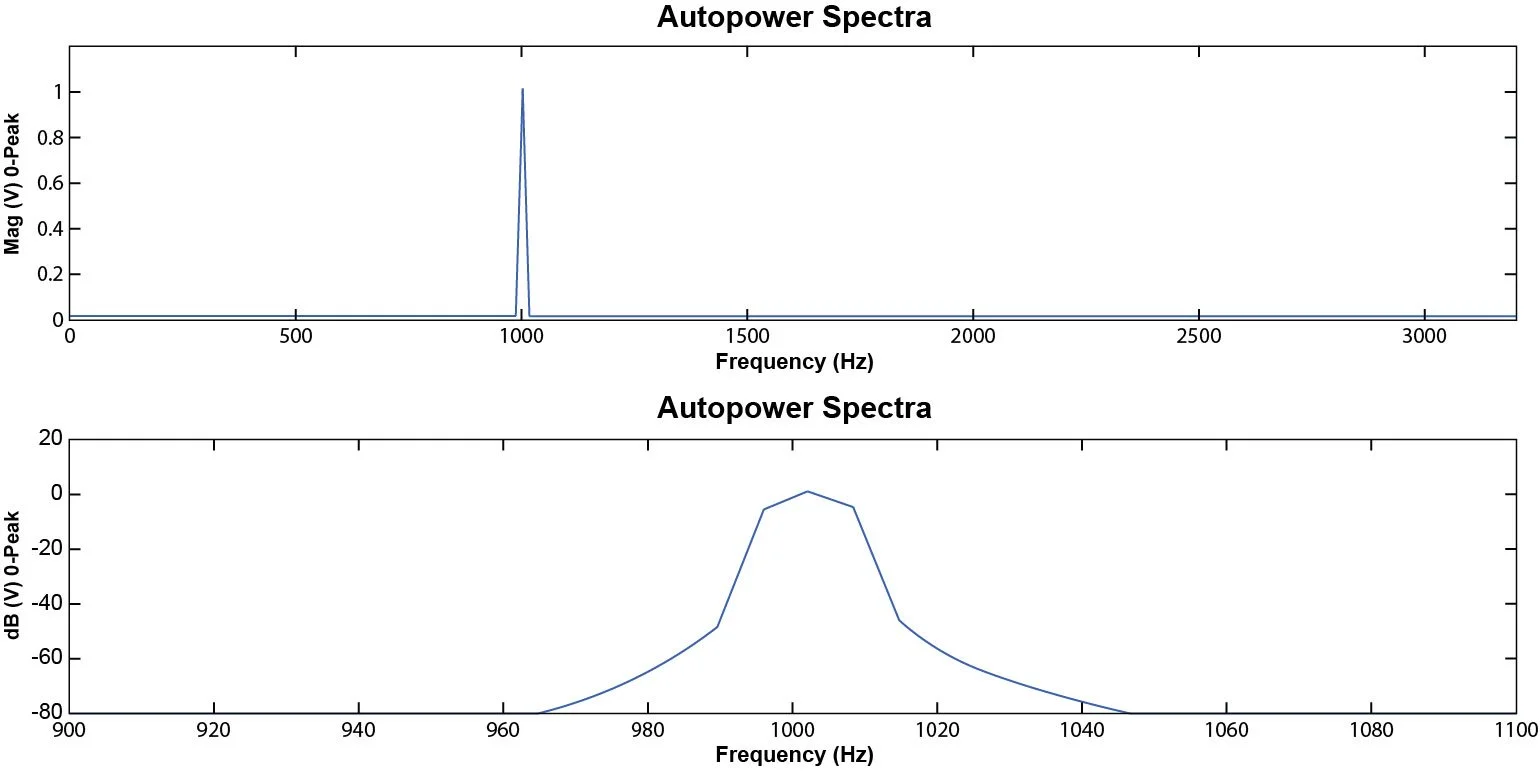
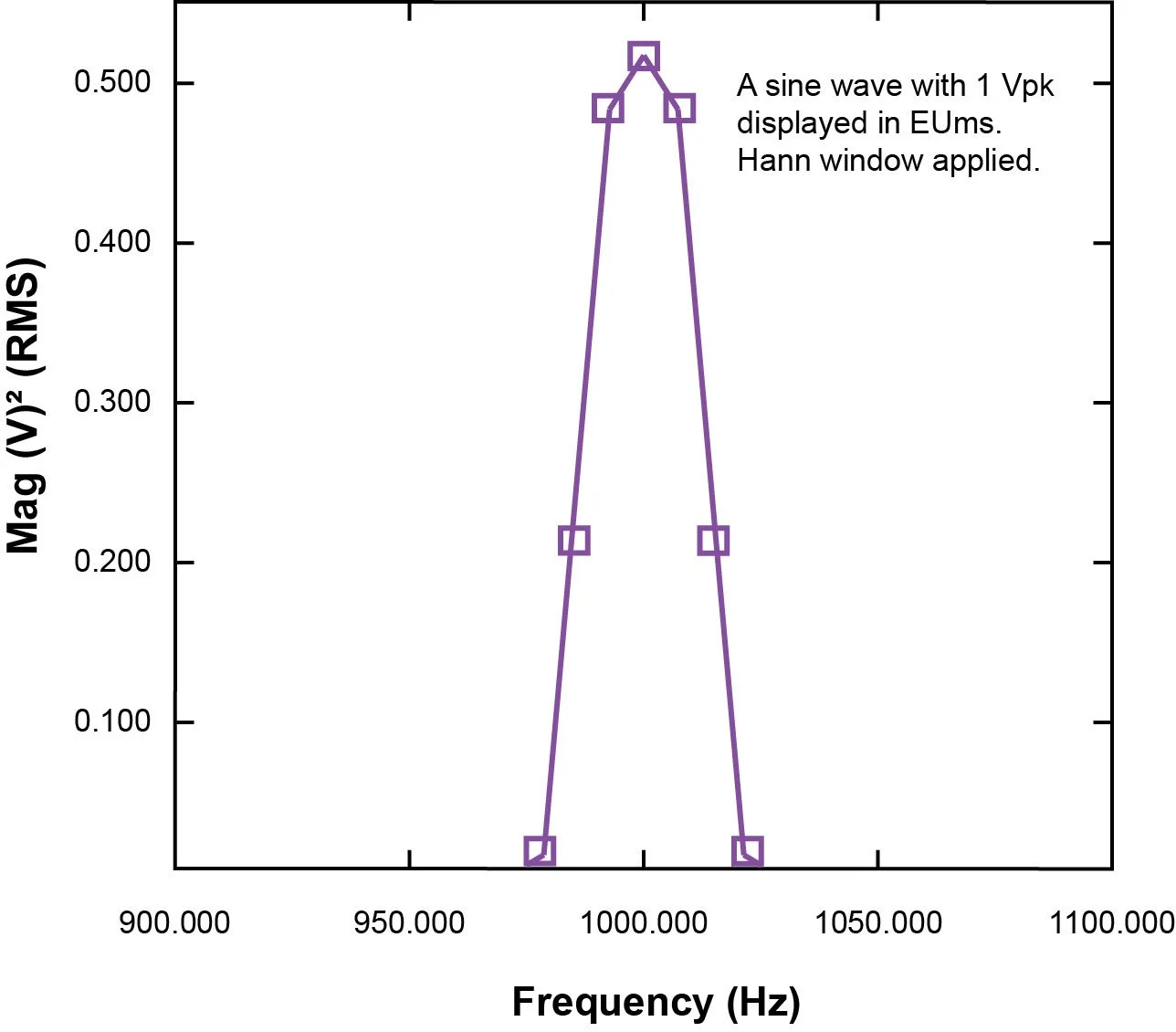
Applying this factor will correct the peak or RMS reading of a sine wave at a specific frequency regardless of which data window is applied. For example, if a 1.0-volt amplitude 1 kHz sine wave sampled at 6.4 kHz is analyzed by a Linear Spectrum with Hann window, the spectral shape in Figure 15 is the result.
Figure 15. 1 kHz sine tone and its corresponding APS.
The top image depicts a digitized time waveform. The sine wave is not smooth because of the low sampling rate relative to the frequency of the signal. However, the well-known Nyquist principle indicates that the frequency estimate from the FFT will be accurate as long as the sampling rate is more than twice of the signal frequency. The frequency spectrum of the period signal will show an accurate frequency and level. Note that a higher sampling rate is required to obtain a more accurate sample of the time waveform.
Figure 16. Hanning windowing function applied to a pure sine tone.
The top graph displayed in Figure 16 is in EUpk, i.e., the peak of the spectrum is scaled to the actual 0 peak level, which is 1.0 in this case. The bottom graph shows the dB scale applied to the same signal. Since 0 dB is used as the reference, the 1.0 Vpk is now scaled to 0.0 dB. The dB display allows users to view the frequency points around the peak caused by the Hanning window.
The linear spectrum is saved internally in the complex data format with real and imaginary parts. Therefore, users should be able to view the real and imaginary parts, or amplitude and phase of the spectrum.
Power Spectrum
Spectral analysis is commonly used to characterize the operation of mechanical and electrical systems. The power spectrum (and power spectral density, PSD), is a popular type of spectral analysis because a “power” measurement in the frequency domain is one that engineers readily accept and apply in their solutions to problems. Single channel measurements (auto-power spectra) and two channel measurements (cross-power spectra) both play important roles.
Power spectrum measurements use window amplitude correction to obtain an un-biased final spectrum amplitude reading at a specific frequency. PSD or energy spectral density (ESD) measurements always use window energy correction to obtain an un-biased spectral density or energy reading.
In addition to the correction factors, spectrum density measurements (PSD and ESD) require normalization in accordance with the equivalent noise bandwidth (ENBW). This accounts for noise leaking into the DFT bin from adjacent bins.
To compute the spectra listed above, the instrument will follow these steps:
Step 1
A window is applied:
x(k) = w (k)x(k)'
where x(k)' is the original data and x(k) is the data used for a Fourier transform.
Step 2
The FFT is applied to x(t) to compute Sx
𝑁−1
𝑆𝑥 = ∑ 𝑥(𝑘)𝑒−𝑗2𝜋𝑘𝑛/𝑁
𝑛=0
Next, the Periodogram method is used to compute the spectra with an area correction using Sx.
Step 3
Calculate the Power Spectrum:
Sxx = 2 ∙ Sx S*x ∙ AmpCorr2 (V2)
Or calculate the Power Spectral Density:
2 ∙ Sxx/ENBW (V2/hz)
or
2 ∙ Sxx ∙ EnergyCorr2 / ∆f
Or calculate the Energy Spectral Density:
(2 ∙ Sxx ∙ T / ENBW) (V2s / Hz)
Where the Equivalent Noise Bandwidth (ENBW), frequency resolution (∆f), and EnergyCorr are defined as:
T is the time duration of the capture, N is the block size, w(n) is the window function and the symbol * is for complex conjugation.
The three power spectral measurements listed above will automatically select the EU as EUrms because only EUrms has a physical meaning related to signal power.
After the power spectra are calculated, the averaging operation will be applied. More details about averaging operations are discussed in the next sections.
Spectrum Types
EDM provides several spectrum types for Linear and Power Spectrum measurements. This section explains the concept of a spectrum type in detail.
First, consider signals with a periodic nature. These signals can be measured from a rotating machine, bearing, gearing, or any physical structure that operates with repetition. In this case, the user would be interested in amplitude changes at fundamental frequencies, harmonics, or sub-harmonics. Users can select a spectrum type of EUpk, EUpkpk or EUrms.
Figure 17. Plot of a periodic signal.
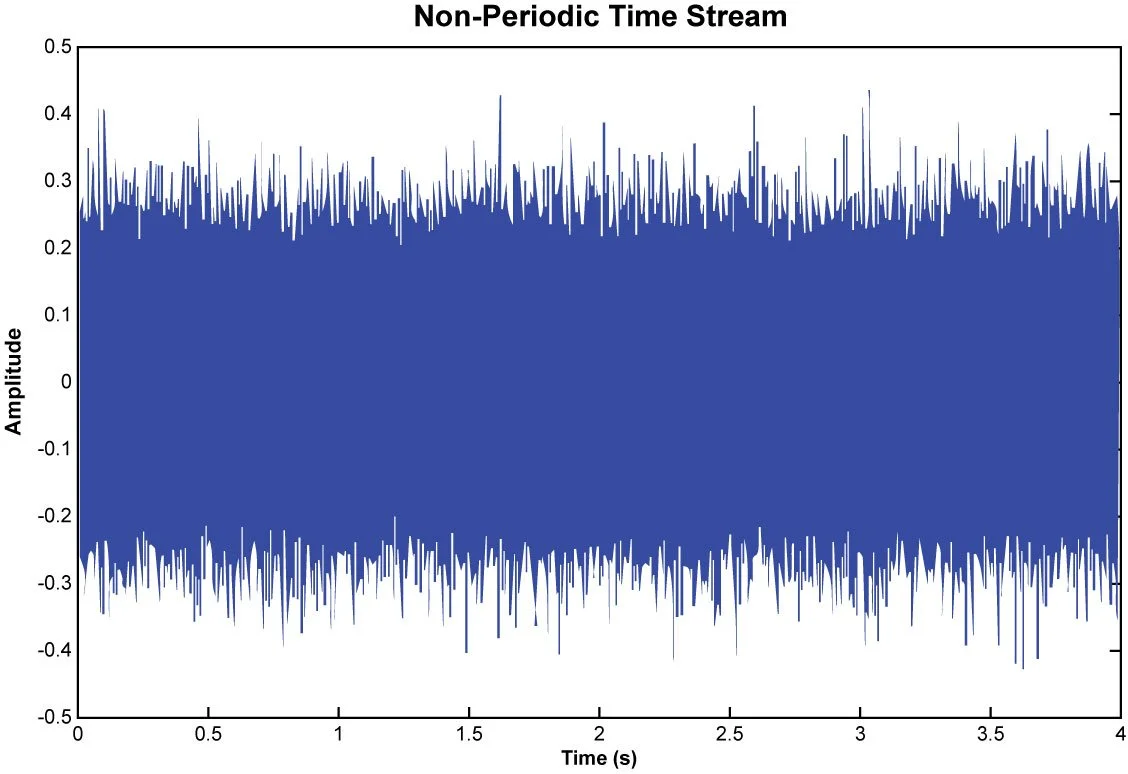
A second scenario might consist of a signal with a random nature that is not necessarily periodic. It does not have obvious periodicity therefore the frequency analysis could not determine the “amplitude” at certain frequencies. However, it is possible to measure the rms level, power level, or power density level over certain frequency bands for such random signals. In this case, the user must select one of the spectrum types of EUrms2/Hz, or EUrms/√Hz, which is called power spectral density, or root-mean squared density.
Figure 18. Plot of a non-periodic signal.
A third scenario might consist of a transient signal. It is neither periodic, nor stably random. In this case, the user must select the spectrum type as EU2/Hz2, which is called energy spectrum.
Figure 19. Plot of a non-periodic and non-random signal.
In many applications, the nature of the data cannot be easily classified. Users should carefully interpret the data when different spectrum types are used. For example, in the environmental vibration simulation, a typical test uses multiple sine tones on top of a random profile, which is called Sine-on-Random. In this type of application, the user must observe the random portion of the data in the spectrum with EUrms2/Hz and the sine portion of the data with EUpk.
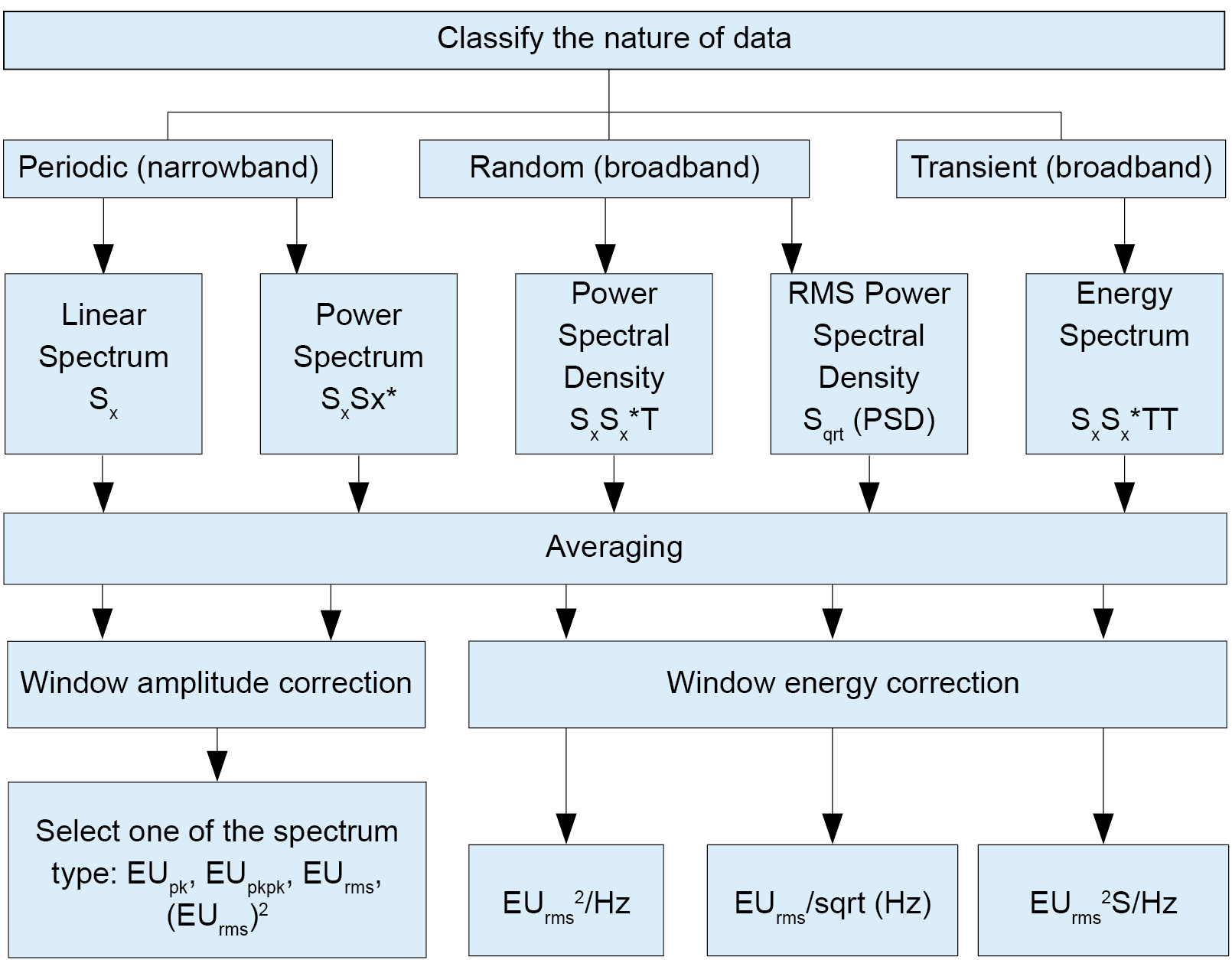
Figure 20 provides a general flow-chart to select one of the measurement techniques and spectrum types for linear or auto spectrum.
Figure 20. Flow chart to determine measurement technique for various signal types.
The following figures illustrate the results of different measurement techniques on a 1-volt pure sine tone. The figures include RMS, Peak or Peak-Peak value for the amplitude, or power value corresponding to its amplitude. Note that these readings can only be applied to a periodic signal. If these measurement techniques were applied to a signal with random nature, the spectrum would not be a meaningful representation of the signal.
EUpk or EUpkpk Amplitude Spectrum
The EUpk and EUpkpk display the peak value or peak-peak value of a periodic frequency component at a discrete frequency. These two spectrum types are suitable for narrowband signals.
Figure 21. Sine wave is measured with EUpeak spectrum unit. The sine waveform has a 1 V amplitude.
EUrms
The EUrms displays the RMS value of a periodic frequency component at a discrete frequency. This spectrum type is suitable for narrowband signals
Figure 22. Sine wave is measured with EUrms spectrum unit. The peak reading is 0.707 V. The sine waveform has a 1 V amplitude.
EU2rms Power Spectrum
The EU2rms displays the power reading of a periodic frequency component at a discrete frequency. This spectrum type is suitable for narrowband signals.
Figure 23. A sine wave is measured with EU2rms spectrum unit. The peak reading is 0.5 V2. The sine waveform has a 1 V amplitude.
EU2/Hz Power Spectal Density
The EU2/Hz is the spectrum unit used in power spectral density (PSD) calculations. The unit is in engineering units squared divided by the equivalent filter bandwidth and provides power normalized to a 1 Hz bandwidth. This is useful for broadband and continuous signals. EU2/Hz and in fact, should be defined as EU2rms/Hz. Many users will commonly shorten it as EU2/Hz.
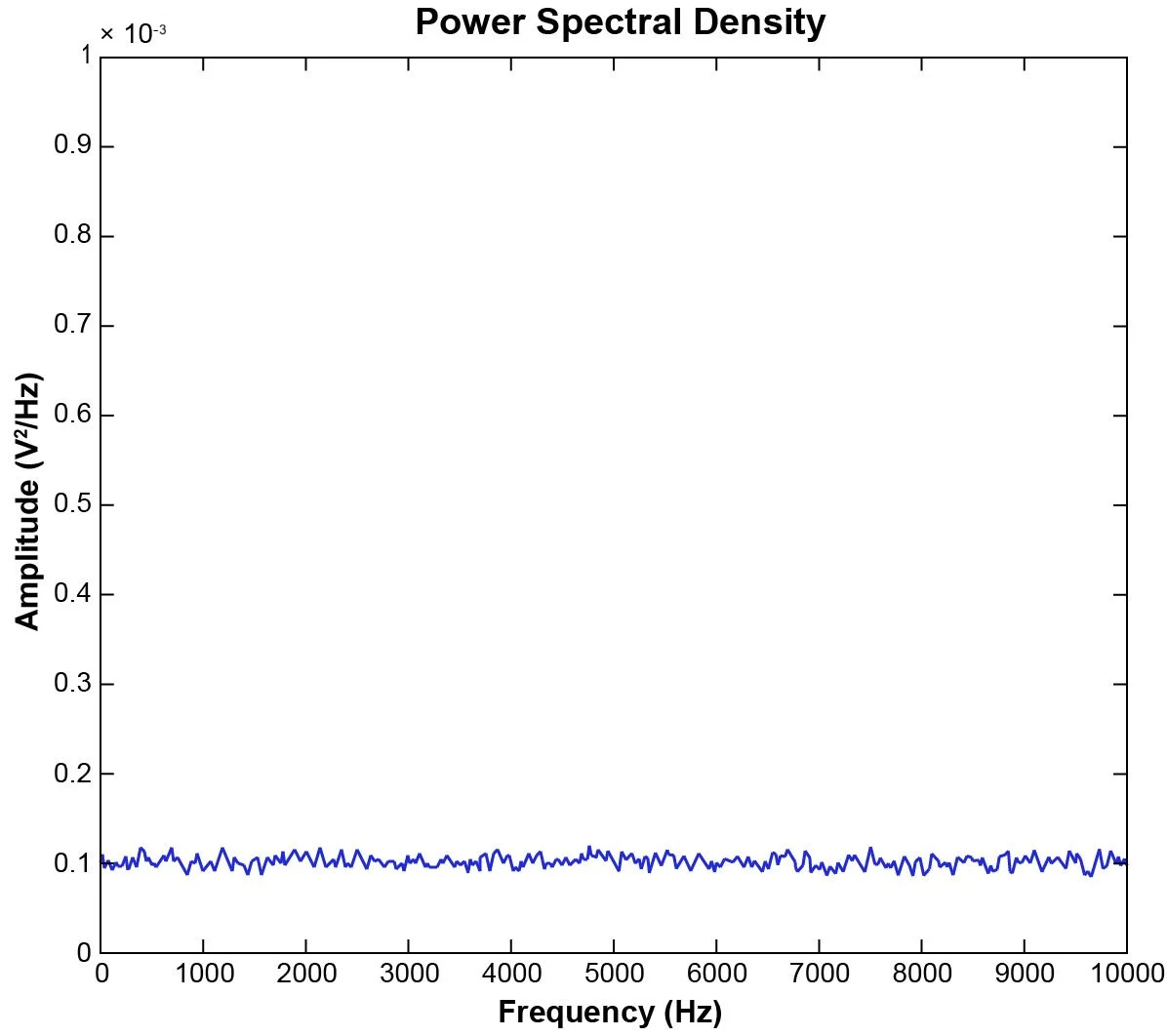
Figure 24. White noise with 1 volt RMS amplitude displays as 100 u V2rms/Hz
Figure 24 shows a white noise signal with 1 Vrms amplitude or 1 V2 in power level. The bandwidth of the signal is approximately 10000 Hz and the V2/Hz reading of the signal is around 0.0001 V2/Hz. The 1 Vrms can be calculated as follows:
EU2S/Hz Energy Spectral Density
The EU2S/Hz displays the signal in engineering units squared divided by the equivalent filter bandwidth, multiplied by the time duration of signal. This spectrum type provides energy normalized to a 1 Hz bandwidth, or energy spectral density (ESD). It is useful for any signals when the purpose is to measure the total energy in the data frame. Figure 25 shows a random signal with a 1 volt RMS level in the ESD format.
Figure 25. Random signal with 1 volt RMS amplitude and Energy Spectral Density format.
The ESD is calculated as follows:
Values for ESD = values of PSD * Time Factor
where the Time Factor = (Block size)/∆f and ∆f is the sampling rate / block size.
Notice that in EU2/Hz, or EU2S/Hz, EU really means the RMS unit of the EU, i.e., EUrms.
It should also be noted that since a window is applied in time domain, which corresponds to a convolution in the linear spectrum, it is not possible to have both a valid amplitude and energy correction at the same time. Use Figure 20 to select the appropriate spectrum types.
In a Linear Spectrum measurement, a signal is saved in its complex data format which includes real and imaginary data. Afterwards, an averaging operation is applied to the linear spectrum. In a Power Spectrum measurement, the averaging operation is applied to the squared spectrum. Different averaging techniques will produce different results for Linear Spectrum and Power Spectrum despite using the same spectrum type.
Spectrum Types selection only applies to Power Spectrum and Linear Spectrum signals. Spectrum Types do not apply to transfer functions, phase functions or coherence functions.
EUrms/√Hz RMS Spectral Density
Similar to Power Spectral Density (PSD), the Root Mean Square (RMS) Spectral Density is commonly used to analyze continuous, stationary, broadband signals.
The RMS Spectral Density, also known as the Root Mean Square Spectrum, represents the square root of the Power Spectral Density. Its unit is typically expressed as EUrms/√Hz , or more simply as EU/√Hz.
When analyzing a noise signal, the spectrum can be presented in either PSD or RMS Spectrum units, which are interchangeable via the following relationship:
RMS Spectral Density (f) = √(PSD(f))
For broadband signals, industry conventions often dictate the choice of spectrum unit. For instance, in typical random vibration controllers, spectra are displayed in PSD format using units such as g2/Hz or (m/s2 )2/Hz. Conversely, when measuring the noise floor of a sensor or instrumentation, the RMS Spectral Density unit is often preferred, with engineering units like V/√Hz or ug/√Hz .
One advantage of the RMS Spectral Density unit over PSD is its intuitive interpretability. RMS values are proportional to linear engineering units, such as voltage or acceleration (g-level), which are easier for humans to comprehend compared to their squared counterparts.
Given the spectrum in either PSD or RMS format and a specified frequency band, the total RMS value or power within that band can be calculated using the following formula:
Or
Where f1 and f2 are the boundaries of the frequency band under consideration.
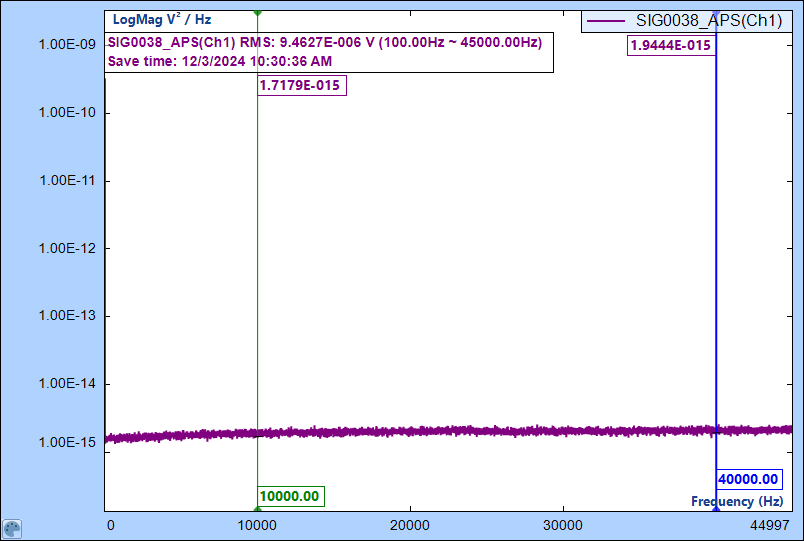
Here is a typical broadband signal that is displayed in two different spectrum units with a vertical cursor enabled. You can see that the value at cursor location has the relationship as RMS(f) = √(PSD(f)):
Figure 26. A typical noise signal displayed in PSD spectral density unit, vertical axis is in logarithmic
Figure 27. The same signal displayed in RMS Spectral Density spectrum unit, vertical axis is in logarithmic
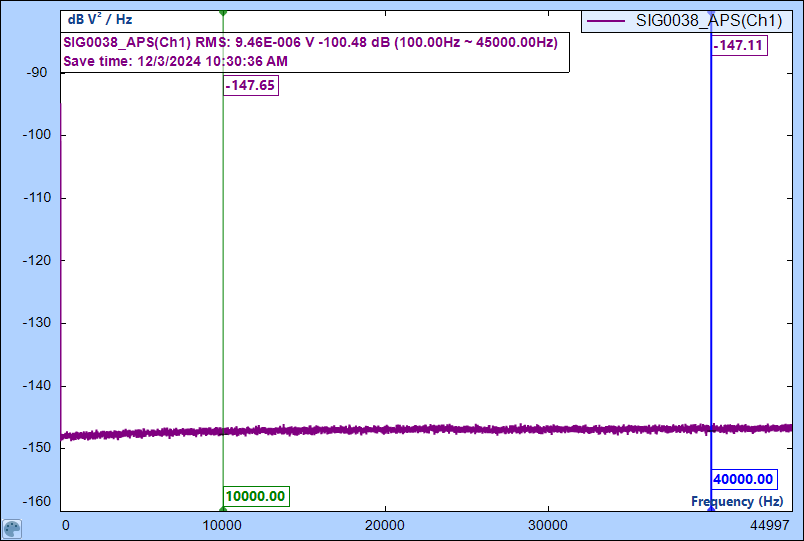
The vertical scaling of RMS Spectral Density or PSD can also be displayed in decibels. When dB is calculated, since PSD is 10Log() based while RMS Spectral Density is 20Log() based, their dB value shall be identical to each other as shown in the following plot with different spectrum units. The plots below show the dB display vertically for both PSD and RMS spectra. The values of dB at any frequency are the same.
Figure 28. The same noise signal displayed in PSD spectral density unit, vertical axis is in dB
Figure 29. The same noise signal displayed in RMS spectral density unit, vertical axis is in dB
Note that in these plots, a software function called dual cursor is enabled. The software can automatically calculate the RMS measure between two cursors.
In this example, RMS value is (9.4627 * 10-6 ) V. In decibel it is 20*Log(9.4627 * 10-6 ) = 20*(Log(9.4627)) + 20* (-6) = -100.48dB. All these values are displayed on the screenshots.
PSD and RMS spectral density types are adequate approach to observe the distribution of random broadband signals. However, these spectral types can not be used to analyze sinusoidal or periodic signals. For periodic signals, please choose EUpk or EUpkpk the amplitude spectrum unit.
Cross Spectrum
Cross spectrum or cross power spectral density is a frequency spectrum quantity computed using two signals, usually the excitation and response of a dynamic system. Cross spectrum is typically used to compute the frequency response function (FRF), transmissibility, or cross correlation function and is not commonly used by itself.
Compute the cross-power spectral density Gyx between channel x and channel y using the following steps:
Step 1, compute the Fourier transform of input signal x(k) and response signal y(k):
Step 2, compute the instantaneous cross power spectral density
Step 3, average the M frames of Szz to get averaged PSD Gxx
Step 4, compute the energy correction and double the value for the single-sided spectra
Frequency Response and Coherence Function
The cross power spectrum method is often used to estimate the frequency response function (FRF) between channel x and channel y. The equation is:
where Gyx is the averaged cross-spectrum between the input channel x and output channel y. Gxx is the averaged auto-spectrum of the input. Either power spectrum, power spectral density or energy spectral density can be used to compute the FRF because of the linear relationship between input and output.
Using the cross-power spectrum method instead of simply dividing the linear spectra between input and output to calculate the FRF will reduce the effect of the noise at the output measurement end, as illustrated in Figure 30.
Figure 30. Frequency response function computation.
The frequency response function has a complex data format. It can be viewed in real and imaginary or magnitude and phase format.
The coherence function is defined as:
where Gyx is the averaged cross-spectrum between the input channel x and output channel y. Gxx and Gyy are the averaged auto-spectrum of the input and output. Power spectrum, power spectral density or energy spectral density can be used here because of the linear relationship between input and output so that any multiplier factors will be cancelled out.
Coherence is a statistical measure of how much of the output is caused by the input. The maximum coherence is 1.0 when the output is perfectly correlated with the input and 0 when there is no correlation between input and output. Coherence is calculated by an average of multiple frames. When it is computed for only one frame, then the coherence function has a meaningless result of 1.0 due to the estimation error of the coherence function.
The coherence function is a non-dimensional real function in the frequency domain. It can only be viewed in real format.
Data Window Selection
Leakage Effect
Windowing of a simple signal, like a sine wave may cause its Fourier transform to have non-zero values (commonly called leakage) at frequencies other than the frequency of this sine. This leakage effect tends to be worst (highest) near sine frequency and least at frequencies farthest from sine frequency. The effect of leakage is easily depicted in the time domain when a signal is truncated. Figure 31 shows the truncation significantly distorted the time signal after data windowing, hence causing a distortion in its frequency domain.
Figure 31. Illustration of the effect of windowing a truncating a signal poorly.
If there are two sinusoids with different frequencies, leakage can interfere with the ability to distinguish them spectrally. If their frequencies are dissimilar, then the leakage interferes when one sinusoid is much smaller in amplitude than the other. That is, its spectral component can be hidden or masked by the leakage from the larger component. But when the frequencies are near each other, the leakage can be sufficient to interfere even when the sinusoids are equal strength; that is, they become undetectable.
There are two possible scenarios where leakage does not occur. The first scenario is when the time capture is long enough to cover the complete duration of the signals. This can occur with short transient signals. For example, in a hammer test, if the time capture is long enough it may extend to the point where the signal decays to zero. In this case, the data window is not needed.
The second scenario is when a periodic signal is sampled to perfectly synchronize with the signal period, so that an integer number of cycles of the signal are always acquired with a block of capture. For example, if a sine wave has a frequency of 1000 Hz and the sampling rate is set to 8000 Hz, each sine cycle would have 8 integer points. If 1024 data points are acquired, then 128 complete cycles of the signal are captured. In this case, with no window applied users will still obtain a leakage-free spectrum.
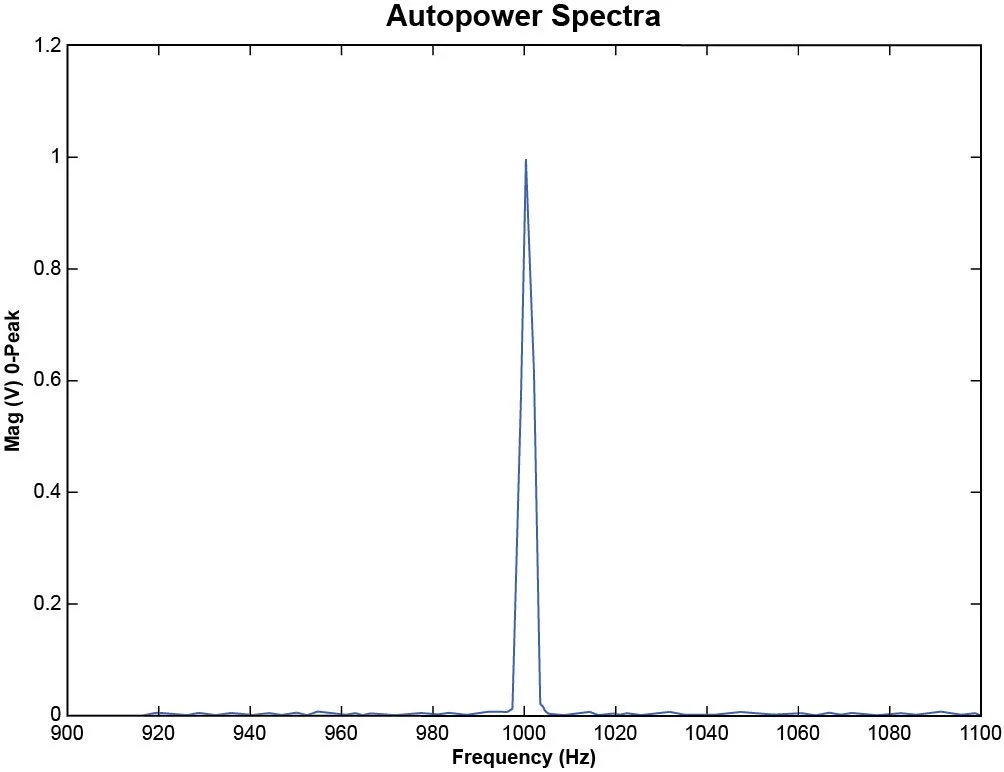
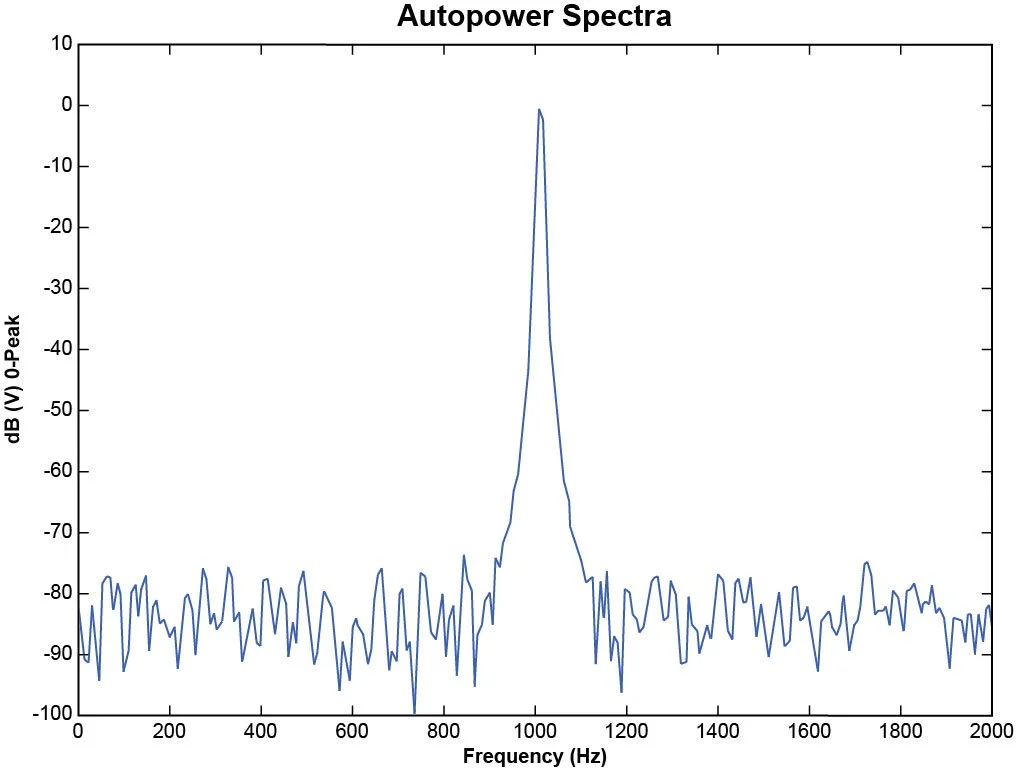
Figure 32 shows a sine signal at 1000 Hz with no leakage resulting in a sharp spike. Figure 33 shows the spectrum of a 1010 Hz signal with significant leakage resulting in a wide peak. The spectrum has significant energy outside the narrow 1010 Hz frequency. It is observed that the energy leaks out into the surrounding frequencies.
Figure 32. Sine spectrum with little leakage.
Figure 33. Sine spectrum with significant leakage.
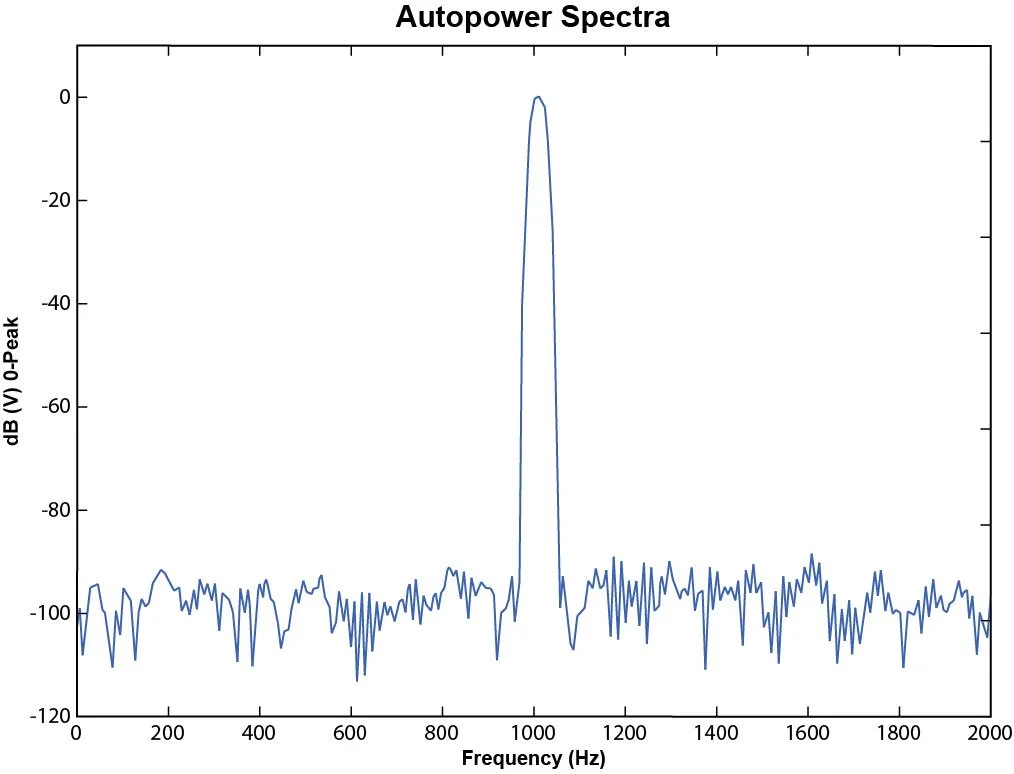
Several windowing functions have been developed to reduce the leakage effect. Figure 34 shows a Flattop window applied to the same sine signal with a frequency of 1010 Hz.
Figure 34. Sine spectrum with Flattop windowing function.
When a Flattop window is used, the leakage effect is reduced. Both the sine peak and noise floor are visible now. However, this type of data windowing operation also results in a “fatter” and less accurate spectrum peak. The remaining sections will discuss how to choose different data windows.
Data Window Formula
This section describes the math formula used for each data window.
Uniform window (rectangular)
w(k) = 1.0
Uniform is identical to no window function.
Hamming window
Hann window
The Hann and Hamming windows belong to the category of "raised cosine" windows, and are respectively named after Julius von Hann and Richard Hamming. The term "Hanning window" is sometimes used to refer to the Hann window but is ambiguous as it is easily confused with Hamming window.
Blackman window
for k = 0~N-1
Flattop window
for k = 0~N-1
Kaiser Bessel window
for k = 0~N-1
Exponential Window
The shape of the exponential window is that of a decaying exponential. The following equation defines the exponential window.
for k = 0~N-1
where N is the length of the window, w(k) is the window value, and final is the final value of the whole sequence. The initial value of the window is one and gradually decays toward zero.
Selecting the Correct Data Window
This section will discuss how to select the data window. Figure 35 shows the spectral shape of four typical windows corresponding to their time waveform.
Figure 35. Spectral shape of common windowing functions.
Observe that the spectral shape of the data window is always symmetric. The spectral shape can be described as a main lobe and several side lobes. (Figure 36)
Figure 36. Window frequency response showing main lobe and side lobes.
The following table lists the characteristics of several data windows.
| Frequency Characteristics of Data Windows | |||
|---|---|---|---|
| Window | –3 dB Main Lobe Width (bins) | –6 dB Main Lobe Width (bins) | Maximum Side Lobe Level (dB) |
| Uniform (none) | 0.9 | 1.2 | –13 |
| Hanning | 1.4 | 2.0 | –32 |
| Hamming | 1.3 | 1.8 | –43 |
| Blackman | 1.6 | 2.3 | –58 |
| Flattop | 2.9 | 3.6 | –44 |
Main Lobe
The center of the main lobe of a window occurs at each frequency component of the time-domain signal. By convention, to characterize the shape of the main lobe, the widths of the main lobe at -3 dB and -6 dB below the main lobe peak describe the width of the main lobe. The unit of measure for the main lobe width is FFT bins or frequency lines.
The width of the main lobe of the window spectrum limits the frequency resolution of the windowed signal. Therefore, the ability to distinguish two closely spaced frequency components increases as the main lobe of the smoothing window narrows. As the main lobe narrows and spectral resolution improves, the window energy spreads into its side lobes, increasing spectral leakage and decreasing amplitude accuracy. A trade-off occurs between amplitude accuracy and spectral resolution.
Side Lobes
Side lobes occur on each side of the main lobe and approach zero at multiples of fs/N from the main lobe. The side lobe characteristics of the smoothing window directly affect the extent to which adjacent frequency components leak into adjacent frequency bins. The side lobe response of a strong sinusoidal signal can overpower the main lobe response of a nearby weak sinusoidal signal.
Maximum side lobe level and side lobe roll-off rate characterize the side lobes of a smoothing window. The maximum side lobe level is the largest side lobe level in decibels relative to the main lobe peak gain.
Guidelines to Select Data Windows
If a measurement can be made without an occurrence of the leakage effect, then do not apply any window (in the software, select Uniform.). As discussed before, this only occurs when the time capture is long enough to cover the whole transient range, or when the signal is exactly periodic in the time frame.
If the purpose of the analysis is to discriminate two or multiple sine waves in the frequency domain, spectral resolution is very critical. Select a data window with a very narrow main slope for these applications. Hanning is a good choice.
If the purpose of the analysis is to determine the amplitude reading of a periodic signal, i.e., to read EUpk, EUpkpk, EUrms or EUrms2, and the amplitude accuracy of a single frequency component is more important than the exact location of the component in a given frequency bin, select a window with a wide main lobe. Flattop windows are often used.
When analyzing transient signals such as impact and response signals, it is better not to use the spectral windows because these windows attenuate important information at the beginning of the sample block. Instead, use the Force and Exponential windows. A Force window is useful in analyzing shock stimuli because it removes stray signals at the end of the signal. The Exponential window is useful for analyzing transient response signals because it damps the end of the signal, ensuring that the signal fully decays by the end of the sample block.
If the nature of the data is random or unknown, select the Hanning window.
Averaging Techniques
Averaging is widely used in spectral measurements. It improves the measurement and analysis of signals that are purely random or mixed random and periodic. Averaged measurements can yield either higher signal-to-noise ratios or improved statistical accuracy.
Typically, three types of averaging methods are available in DSA products. They are:
Linear Averaging
Exponential Averaging
Peak-Hold
Linear Averaging
In linear averaging, each set of data (a block) contributes equally to the average. The value at any point in the linear average is given by the equation:
Averaged = Sum of blocks/N
N is the total number of the blocks. The advantage of this averaging method is that it is faster to compute and the result is un-biased. However, this method is suitable only for analyzing short signal records or stationary signals since the average tends to stabilize. The contribution of new blocks eventually will cease to change the value of the average.
A target average number is usually defined. The algorithm is made so that before the target average number is reached, the process can be stopped, and the averaged result can still be used.
When the specified target averaging number is reached, the instrument usually will stop the acquisition and wait for instructions to perform another round of data acquisition.
Moving Linear Averaging
n a regular Linear Average, the data rate of the output of the averaging operator is only 1/N of that of the original signal. Therefore, more averages take longer to compute, and measurement time is increased. Moving Linear Averaging can reduce the overall measurement time. Moving Linear Averaging uses overlapped input data points to generate more than 1/N results within a period of time. The advantage is a resulted trace update time that can be much shorter than the linear averaging period.
Moving Linear Average is computed by
Where x[k] is the input data, with a sampling rate of T,y[n] as the output data, with Trace Update rate ∆T,Average(T) as the period of Linear Average and , N as the total samples used for Linear Average.N = AverageT/T
The Moving Linear Averaging is illustrated in Figure 37. Assume the averaging period is AverageT but the progressive time for each averaging operation is deltaT, the output buffer will have a data range of deltaT instead of AverageT.
Figure 37. Illustration of a moving linear average.
The Moving Linear Average is useful in many situations. For example, in Sound Level Meter, Leq is defined as a linear averaged value over a long period of time, such as 1 second to 24 hours. Assuming the AverageT is 1 hour, without a moving linear average, in a 24 hour period, only 24 readings are obtained. This is not very useful. Moving averaging obtains readings every 1 second, for the linear averaging of the past 1 hour.
Exponential Averaging
In exponential averaging, blocks do not contribute equally to the average. A new block is weighted more heavily than old ones. The value at any point in the exponential average is given by:
where y[n] is the nth average and x[n] is the nth new block. α is the weighting coefficient. Usually, α is defined as 1/(Number of Averaging). For example in the instrument, if the Number of Averaging is set to 8 and the averaging type is selected as exponential averaging, then α =1/8.
The advantage of this averaging method is that it can be used indefinitely. That is, the average will not converge to some value and stay there, as is the case with linear averaging. The average will dynamically respond to the influence of new blocks and gradually ignore the effects of old blocks.
Exponential averaging simulates the analog filter smoothing process. It will not reset when a specified averaging number is reached.
A drawback of exponential averaging is that a large value may embed too much memory into the average result. If there is a transient large value as input, it may take a long time for y[n] to decay. On the contrary, the contribution of small input value of x[n] will have little impact to the averaged output. Therefore, an exponential average fits a stable signal better than a signal with large fluctuations.
Peak-Hold
This method, technically speaking, does not involve averaging in the strict sense of the word. Instead, the “average” produced by the Peak-Hold method produces a block that at any point represents the maximum envelope among all the component blocks. The equation for Peak-Hold is:
Peak-Hold is useful for maintaining a record of the highest value attained at each point throughout the sequence of ensembles. Peak-Hold is not a linear math operation so it should be used carefully. It is acceptable to use Peak-Hold in auto-power spectrum measurements, but meaningful results for FRF or Coherence measurements are not acquired using Peak-Hold.
Peak-Hold averaging will reset after a specified averaging number is reached.
Linear Spectrum versus Power Spectrum Averaging
Averaging can be applied to either linear spectrum or power spectrum. To reduce the spectral estimation variance, use power spectral averaging. To extract repetitive or periodic small signals from a noisy signal, use triggered capture and average them in linear spectral domain. Linear Spectrum averaging must be performed on a triggered event so that the time signal of one average is correlated with other similar measurements. Averaging in the Linear Spectrum domain does not make sense without a time synchronizing mechanism. Linear spectrum averaging is also called Vector averaging. It averages the complex FFT spectrum. (The real part is averaged separately from the imaginary part.) This can reduce the noise floor for random signals since they are not phase coherent from time block to time block.
Power Spectrum Averaging is also called RMS Averaging. RMS averaging computes the weighted mean of the sum of the squared magnitudes (FFT times its complex conjugate). The weighting is either linear or exponential. RMS averaging reduces fluctuations in the data but does not reduce the actual noise floor. With a sufficient number of averages, a very good approximation of the actual random noise floor can be displayed. Since RMS averaging involves magnitudes only, displaying the real or imaginary part, or phase, of an RMS average has no meaning and the power spectrum average has no phase information.
Table 1 provides a summary of the averaging methods described above.
Table 1. Summary of Averaging Methods.
| Frequency Characteristics of Data Windows | |||
|---|---|---|---|
| Window | –3 dB Main Lobe Width (bins) | –6 dB Main Lobe Width (bins) | Maximum Side Lobe Level (dB) |
| Uniform (none) | 0.9 | 1.2 | –13 |
| Hanning | 1.4 | 2.0 | –32 |
| Hamming | 1.3 | 1.8 | –43 |
| Blackman | 1.6 | 2.3 | –58 |
| Flattop | 2.9 | 3.6 | –44 |
Spectrum Estimation Error
Users may wonder how much confidence should have when taking a spectral measurement. This is an academic topic that can go very deep. First, classify the signal types. The spectrum estimation can be very accurate with very few averaging if the user is measuring a deterministic signal. More averaging must be used if the signal has a random nature, with partially random, or significant measurement noise.
Assuming the time data is captured from a stationary random process and various spectra is calculated using window, FFT and averaging techniques, we can trust the measured spectra can be measured by a statistical quantity, standard deviation. The following table provides a few useful equations to compute the standard deviation of the spectra when linear averaging is used:
| Functions being estimated | Standard Deviation |
|---|---|
| Auto-spectrum Gxx |  |
| Cross-spectrum |Gyx| |  |
| Coherence Function γ2yx |  |
| Frequency Response Function Hyx |  |
where n is the average number in linear averaging. The transfer function is computed in the cross-power spectrum method as presented earlier.
Assume a signal is random and has an expected power spectral density at 0.1 V2/Hz. The goal of a measurement is to average a few power spectra and to estimate such an expected value. If the average number is 1, meaning, with no average, the standard deviation of the error of such a measurement will be 100%. When we average two blocks of auto power spectra, the standard deviation of the error will become 1/(√2) = 70.7% When the average number is increased to 100, the standard deviation of the error of the reading is 10%. This means that the reading is likely in the neighborhood of (0.1±0.01) V2/Hz.
Now if this signal has a deterministic nature, say a sine wave, the spectral estimation error will only be applied to the random portion, i.e., the noisy portion, of this signal.
Overlap Processing
To increase the speed of spectral calculation, overlap processing can be used to reduce the measurement time. The diagram in Figure 38 shows how the overlap is realized.
Figure 38. Illustration of overlap processing.
As shown in Figure 38, when a frame of new data is acquired after passing the Acquisition Mode control, only a portion of the new data will be used. Overlap calculation will speed up the calculation with the same target average number. The percentage of overlap is called overlap ratio. 25% overlap means 25% of the old data will be used for each spectral processing. 0% overlap means that no old data will be reused.
Overlap processing can improve the accuracy of spectral estimation. This is because when a data window is applied, some useful information is attenuated by the data window on two ends of each block. However, it is not true that the higher the overlap ratio the higher the spectral estimation accuracy. For Hanning window, when the overlap ratio is more than 50%, the estimation accuracy of the spectra will not be improved.
Another advantage of applying overlap processing is that it helps update the display more quickly.
Single Degree of Freedom System
This section briefly discusses the single degree of freedom (SDOF) system as background knowledge for the frequency response function and damping estimation methods.
The vibration nature of a mechanical structure can be decomposed into multiple, relatively independent Single-Degree-of-Freedom systems. Each SDOF system can be modeled as a mass fixed to the ground by a spring and damper in parallel as shown in Figure 39. The frequency response function (FRF) of this mechanical system is also shown.
Figure 39. SDOF system and its frequency response.
The differential equation of motion for this system is given by
where m is the mass, k is the spring stiffness and c is the damping coefficient.
The natural frequency ωn and damping ratio ζ can be calculated from the system parameters as
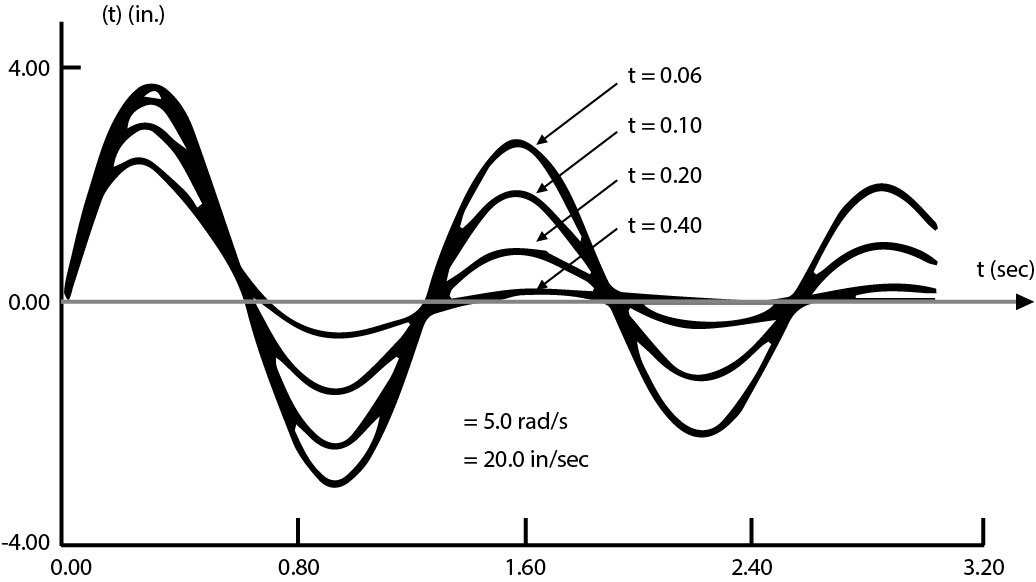
The natural frequency, ωn, is in units of radians per second (rad/s). The typical units displayed on a digital signal analyzer are in Hertz (Hz). The damping ratio, ζ, can also be represented as a percent of critical damping – the damping level at which the system experiences no oscillation. This is a more common understanding of modal damping. Figure 40 illustrates the response of a SDOF system to a transient excitation showing the effect of different damping ratios.
Figure 40. Step response of a SDOF system with different damping ratios.
A SDOF system with light damping factor will have longer oscillation in a transient process. This is why the exponential window can be selected to reduce the leakage effect in its spectral analysis.
dB and Linear Magnitude
Amplitude or power spectra are most often shown in the logarithmic unit decibels (dB). It is easy to view wide dynamic ranges using this unit of measure; that is, it is easy to see small signal components in the presence of large ones. The decibel is a unit of ratio and is computed as follows.
where Power is the measured power and Pref is the reference power.
Use the following equation to compute the ratio in decibels from amplitude values.
where Ampl is the measured amplitude and Aref is the reference amplitude.
When using amplitude or power as the amplitude-squared of the same signal, the resulting decibel level is exactly the same. Multiplying the decibel ratio by two is equivalent to having a squared ratio. Therefore, the same decibel level and display is obtained regardless of whether the amplitude or power spectrum is used.
As shown in the preceding equations for power and amplitude, a reference must be supplied for a measure in decibels. This reference then corresponds to the 0 dB level. Different conventions are used for different types of signals. A common convention is to use the reference 1 Vrms for amplitude or 1 Vrms squared for power, yielding a unit in dBV or dBVrms. In this case, 1 Vrms corresponds to 0 dB. Another common form of dB is dBm, which corresponds to a reference of 1 mW into a load of 50 Ω for radio frequencies where 0 dB is 0.22 Vrms, or 600 Ω for audio frequencies where 0 dB is 0.78 Vrms.
Figure 41 shows a sine wave with 1 V amplitude displayed in dB. It shows the peak value of this sine wave as 0 dB since the reference is 1 Vpk.
Figure 41. 1-Vpk sine signal in frequency domain with dB scaling.
Another display format is called Log, or LogMag. The Log display shows the signal scaled logarithmically with the grid values and cursor readings in actual engineering values. Figure 42 depicts the same signal in LogMag.
Figure 42. 1-Vpk sine signal in frequency domain with LogMag scaling.
When the dB reference is not specified, the dB reference is 1.0 engineering unit. In acoustics applications, the dB reference for the sound pressure value is set to 20 uPa. The same input signal will result in different dB readings when the dB reference is changed.
Transient Capture and Hammer Testing
Transient Capture
The previous sections discussed how the acquisition mode can be defined and selected on the DSA (Dynamic Signal Analyzer) device. This chapter will demonstrate how to use DSA to conduct hammer testing. Hammer testing refers to impact or bump testing that is conducted using an impact hammer to apply an impulsive force excitation to a test article while measuring the response excitation from an accelerometer or other sensor. This type of measurement is a transient event that usually requires triggering, averaging, and windowing. First, let’s briefly review the Transient Capture function on DSA.
Transient Capture is one of the most commonly used functions for dynamic data acquisition. (Figure 43) In DSA, the Transient Capture function is implemented by setting up the Acquisition Mode. Acquisition Mode defines how to transform the time streams into block-by-block time signals. It sets the trigger and the overlapping processing. The instrument acts as a data recorder before the Acquisition Mode stage. After Acquisition Mode, it acts as a signal analyzer.
Figure 43. Transient capture operation on DSA.
Besides Acquisition Mode, the user must first enable at least one time stream as a trigger candidate in the DSA. Trigger candidates are time streams that can be selected as a trigger source. The names of these trigger candidates will be passed to the DSA. During runtime, one of the trigger source candidates must be selected as the trigger source.
Impact Hammer Testing
Impact hammer testing is typically conducted with a signal analyzer to measure FRFs of the device under test. The FRFs can be used to determine the modal properties of the device such as the natural frequencies and damping ratios. Data can be exported to compute mode shapes with third party modal analysis software.
An impact hammer test is the most common method of measuring FRFs. The hammer imparts a transient impulsive force excitation to the device. The impact is intended to excite a wide range of frequencies so that the DSA can measure the vibration of the device across this range of frequencies. The bandwidth or frequency content of the excitation input depends on the size and type of impact hammer that is used. The dynamic force signal is recorded by the DSA. After the impact, the device vibrations are measured with one or more accelerometers or another sensor and are recorded by the DSA. The DSA then computes the FRF by comparing the force excitation and the response acceleration signals. Impact testing is depicted in Figure 44.
Figure 44. Illustration of a typical impact test and signal processing.
The following equipment is required to perform an impact test:
An impact hammer to excite the structure. We recommend using an impact hammer with an IEPE output for DSA applications, which allows the hammer to be connected directly to the analyzer without an extra signal conditioning unit.
One or multiple accelerometers that are fixed on the structure. Again, IEPE accelerometers can be used directly with the DSA and without an additional signal conditioning unit.
Dynamic Signal Analyzer, either CoCo or Spider hardware platform
EDM Modal software can be used to extract the resonance frequencies, damping factors of the structure, and modal shapes. The mode shapes can be used to animate the vibration modes.
A wide variety of structures and machines can be impact tested. Different sized hammers are required to provide the appropriate impact force, depending on the size of the structure; small hammers for small structures, large hammers for large structures. Realistic signals from a typical impact test are illustrated in Figure 45.
Figure 45. Typical impact test data. The top left shows excitation force impulse time signal, top right shows response acceleration time signal and bottom shows FRF spectrum.
Impact Test Analyzer Settings
The following settings are used for impact testing.
Trigger Setup including trigger level and pre-trigger delay are used to capture the transient signal for FRF processing. It is important to capture the entire short transient signal in the sampling window of the FFT analyzer. To ensure that the entire signal is captured, the analyzer must be able to capture the impulse and impulse response signals prior to the occurrence of the impulse with the pre-trigger.
Force & Exponential Windows. Two common time domain windows that are used in impact testing are the force and exponential windows. These windows are applied to the signals after they are sampled, but before the FFT is computed in the analyzer.
The force window is used to remove noise from the impulse (force) signal. Ideally, an impulse signal is non-zero for a small portion of the sampling window, and zero for the remainder of the window time period. Any non-zero data following the impulse signal in the sampling window is assumed to be measurement noise. CoCo has a unique way to implement the force window. This was discussed in the data windowing section in the previous chapter.
The exponential window is applied to the impulse response signal. The exponential window is used to reduce leakage in the spectrum of the response.
Accept/Reject: Because accurate impact testing results depend on the skill of the operator, FRF measurements should be made with averaging, a standard capability in all modern FFT analyzers. FRFs should be measured using at least 4 impacts per measurement. Since one or two of the impacts during the measurement process may be bad hits (too hard causing saturation, too soft causing poor coherence or a double hit causing distortion in the spectrum), an FFT analyzer designed for impact testing should have the ability to accept or reject the result of each impact after inspecting the impact signals. An accept/reject capability saves a lot of time during impact testing since users are not required to redo all measurements in the averaging process after one bad hit.
Modal Damping Estimation. The width of the resonance peak is a measure of modal damping. The resonance peak width should also be the same for all FRF measurements, meaning that modal damping is the same in every FRF measurement. A good analyzer should provide an accurate damping factor estimate. CoCo uses a curve fitting algorithm to estimate the damping factor. The algorithm reduces the inaccuracy caused by the poor spectrum resolution or noise.
Modal Frequency Estimation. The analyzer must provide the capability of estimating the resonance frequencies. DSA uses an algorithm to identify the resonance frequencies based on the FRF.
Time Domain Analysis
Constraints related to analysis in the time-domain domain diverge from those in the frequency domain, especially concerning the choice of sampling rate. As an example, constructing Shock Response Spectrums involves using measurements of peak values observed in the time-domain. A shock pulse is a transient event and does not exhibit periodic behavior. To capture the peak value of a shock pulse, sampling at the Nyquist rate may be too low. This is better understood through an illustration.
Consider the following half-sine shock pulse in Figure 46.
Figure 46. Plot of a half-sine shock pulse as a function of time.
Now, the goal is to sample the pulse at a rate sufficient to capture the peak amplitude. Suppose the pulse is sampled at 80 Hz, the obtained waveform is shown in Figure 47.
Figure 47. Plot of a shock pulse and its sampled version acquired at 80 Hz.
The sampling rate is not fast enough to capture the peak in this case. A shock response spectrum generated with the sampled data would be inaccurate. Now, if the pulse was sampled at 400 Hz instead of 80 Hz, the waveform depicted in Figure 48 would have been captured.
Figure 48. Plot of a shock pulse and its sampled version acquired at 400 Hz.
By sampling at 400 Hz, the collected samples are in proximity to the peak of the original waveform, allowing us to accurately construct a shock response spectrum. In general, for time-domain analysis, it is recommended to sample signals at a rate 10 times higher than the anticipated highest frequency component. This is so that the peak measurement of the pulse is within 5% of its true peak.
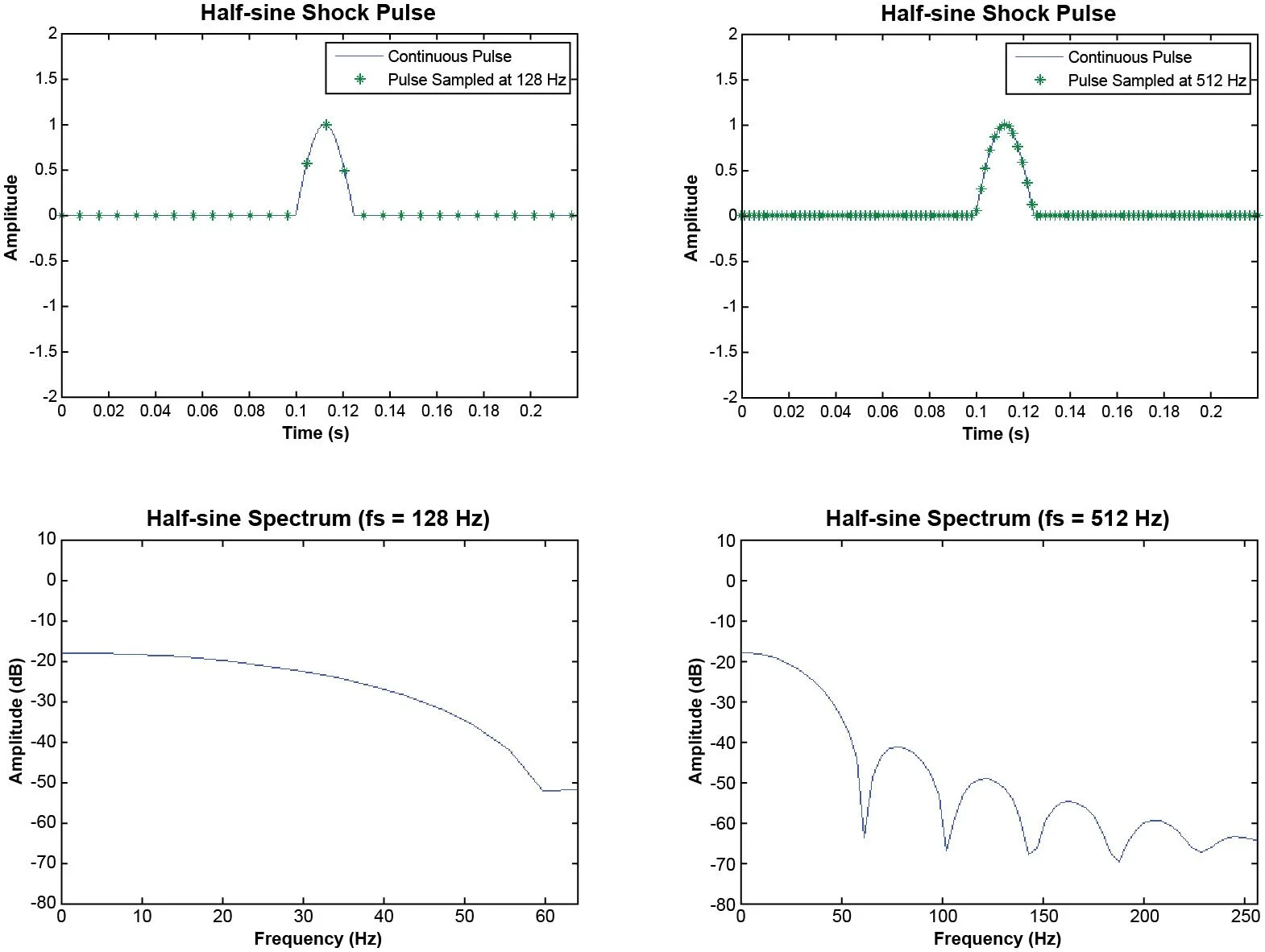
Moreover, a high sampling rate is necessary to capture high-frequency events. Transients are typically short-lived, abrupt changes in a signal, like a sudden spike. These rapid changes that characterize transients in the time-domain correspond to high-frequency components in the frequency domain. Thus, to accurately measure the composition of the energy in a transient signal, a high sampling rate is required to generate a spectrum with a range wide enough to accommodate the high-frequency components. Figure 49 illustrates the disparity in detail between the two spectra resulting from the variations in sampling rates.
Figure 49. Frequency spectra of a half-sine signal sampled at 128 Hz and 512 Hz.
References
To understand the topics of this article, we found the following three books to be very helpful:
Julius S. Bendat and Allan G. Piersol, Random Data, Analysis and Measurement Procedures, 2nd Edition, Wiley-Interscience, New York, 1986.
Julius S. Bendat and Allan G. Piesol, Engineering Applications of Correlation and Spectral Analysis, 2nd Edition, Wiley-Interscience, New York, 1993.
Sanjit K. Mitra and James F. Kaiser, Ed. Handbook for Digital Signal Processing, Wiley-Interscience, New York, 1993.