Frequency Response Function
FFT Spectral Analysis
Frequency Response Function (FRF) is a commonly used measurement type of the Dynamic Signal Analyzer. FRF is defined as the ratio of response i.e. acceleration, velocity, or displacement with respect to the excitation force which is the reference.
To measure the FRF, there are three different methods using EDM DSA software:
FFT based
Swept sine based
Multi-resolution spectrum based
View Crystal Instruments Complete Dynamic Signal Analysis Solutions
Figure 1. Frequency Response Function
FFT Analysis Solutions
With FFT based FRF measurement, typically broadband excitation, i.e., impact pulse, or white noise signal is used to excite the device under test. This method is commonly used and easy to set up.
Swept Sine Based
With Sine or Swept Sine based excitation, the energy concentrates in the current frequency and will yield the FRF with high fidelity.
Specification for Swept sine based FRF:
- User specified Low/High/Start frequency
- Sweeping Rate: Log (Oct/Min): 0.001 to 120; Log (Dec/Min): 0.001 to 40; Linear (Hz/Sec): 0.001 to 120
- Sweep Rate Control: Oct/Min, Hz/Sec, Dec/Min, Sweeps/Min, Sweep Duration/Sweeps
- Tracking Filters: Proportional: 7% – 100%; Fixed (Hz): 1– 500 Hz
- Frequency Resolution: as fine as 0.000001 Hz
Multi-resolution Spectrum (MR) FRF
Crystal Instruments created the Multi-resolution (MR) Spectrum based FRF technique. With its unique processing on the low band FRF, the frequency resolution at the low frequency band can be much higher than the broadband. Due to the nature of that damping ratio is similar for the low and high frequency bands, this higher resolution FRF will yield the FRF signals which could result in the damping ratio be measured several times accurate compared to the classical FRF measurement.
Specification for Multi-resolution spectrum based FRF
- Output: White noise with user specified Amplitude
- MR frequency transition (as ratio of Fa): ½, ¼, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256
- Average type: exponential; linear; Peak
- Average number: user defined
For FRF measurement, H1, H2, H3, and Hv evaluations are all supported. This is useful when users are dealing with the system's different sources of noise.
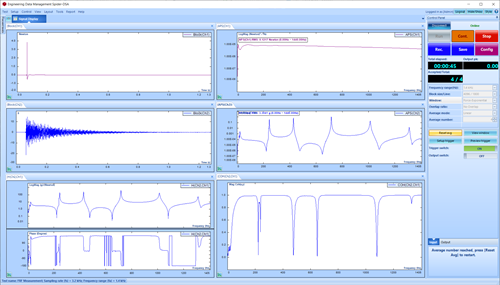
Figure 2. Typical FRF measurement
Monitoring Through EDM Cloud
EDM Cloud allows users to continuously monitor input channels and status information. Crystal Instruments provides user accounts with convenient cloud storage space for uploading data. All tests in EDM-DSA support status are checked through EDM Cloud. FFT Spectral Analysis is widely used for monitoring applications.
The EDM Cloud website is located at https://cloud.go-ci.com. Users can access EDM Cloud from anywhere in the world to check the status of past and current tests. A secure login flow ensures the status can only be checked by authorized personnel with proper credentials. Multiple logins for accessing the same Cloud account is available.
|
|
|
|
|
|
FRF Data Acquisition Hardware
Crystal Instruments provides a family of Spider and CoCo data acquisition hardware ranging from 4 input channels to 512 input channels, with sample rates of 102.4 kHz or 256 kHz. Post Analyzer takes the recorded data files and performs the spectrum analysis offline.
The following table details features of DSA FRF measurement provided with each hardware platform.
FFT based:
| Hardware Platform | Spider-20/20E | Spider-20H/20HE/20i | Spider-80Xi | Spider-80Hi/Ci | CoCo-70X | CoCo-80X | CoCo-90X | PA |
|---|---|---|---|---|---|---|---|---|
| Max channels | 4-256 | 4-256 | 8-512 | 8-512 | 4 | 8 | 16 | up to 512 |
| Max freq range | 46 kHz | 115.2 kHz | 46 kHz | 115.2 kHz | 46 kHz | 46 kHz | 46 kHz | 115.2 kHz |
| Max line | 28800 | 28800 | 28800 | 28800 | 28800 | 28800 | 28800 | 28800 |
| Data window | Hann, Hamming, Flattop, Uniform, Kaiser-Bessel, Blackman, Force, Exponential, Force-Exponential | |||||||
| Signals measured | Linear spectrum, Auto power spectrum, Frequency response function, Coherence, Cross power spectrum, Phase spectrum | |||||||
| Typical Excitation | hammer impulse, White noise (Random), Pink noise, Shaped random, Sine, Swept sine, Chirp | |||||||
| Dynamic range | 100 dB | 100 dB | 160 dB | 160 dB | 160 dB | 160 dB | 160 dB | 160 dB |
Swept Sine based:
| Hardware Platform | Spider-20/20E | Spier-20H/20HE/20i | Spider-80Xi | Spider-80Hi/Ci | CoCo-70X | CoCo-80X | CoCo-90X |
|---|---|---|---|---|---|---|---|
| Max channels | 4-256 | 4-256 | 8-512 | 8-512 | 4 | 8 | 16 |
| Max freq range | 30 kHz | 30 kHz | 30 kHz | 30 Hz | 30 kHz | 30 kHz | 30 kHz |
| Signals measured | Time stream, Time block, Linear spectrum, Frequency response function | ||||||
| Dynamic range | 100 dB | 100 dB | 160 dB | 160 dB | 160 dB | 160 dB | 160 dB |
Multi-resolution Spectrum based:
| Hardware Platform | Spider-20/20E | Spier-20H/20HE/20i | Spider-80Xi | Spider-80Hi/Ci |
|---|---|---|---|---|
| Max channels | 4-256 | 4-256 | 8-512 | 8-512 |
| Max freq range | 46 kHz | 115.2 kHz | 46 kHz | 115.2 kHz |
| Max line | 28800 | 28800 | 28800 | 28800 |
| Data window | Hann, Hamming, Flattop, Uniform, Kaiser-Bessel, Blackman, Force, Exponential, Force-Exponential | |||
| Signals measured | Linear spectrum, Auto power spectrum, Frequency response function, Coherence, Cross power spectrum, Phase spectrum | |||
| Typical Excitation | White noise (Random), Pink noise, Shaped random, Sine, Swept sine, Chirp | |||
| Dynamic range | 100 dB | 100 dB | 160 dB | 160 dB |
