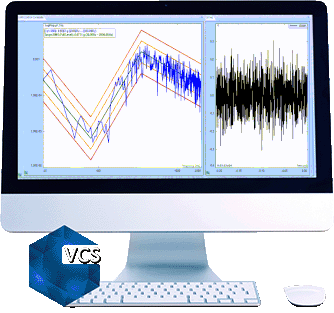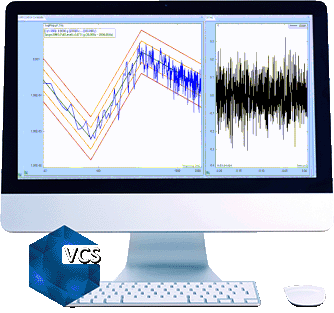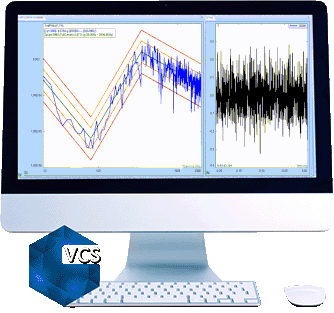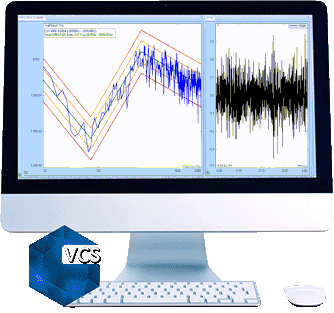
Random Vibration Testing
Single Axis Shaker Vibration Testing
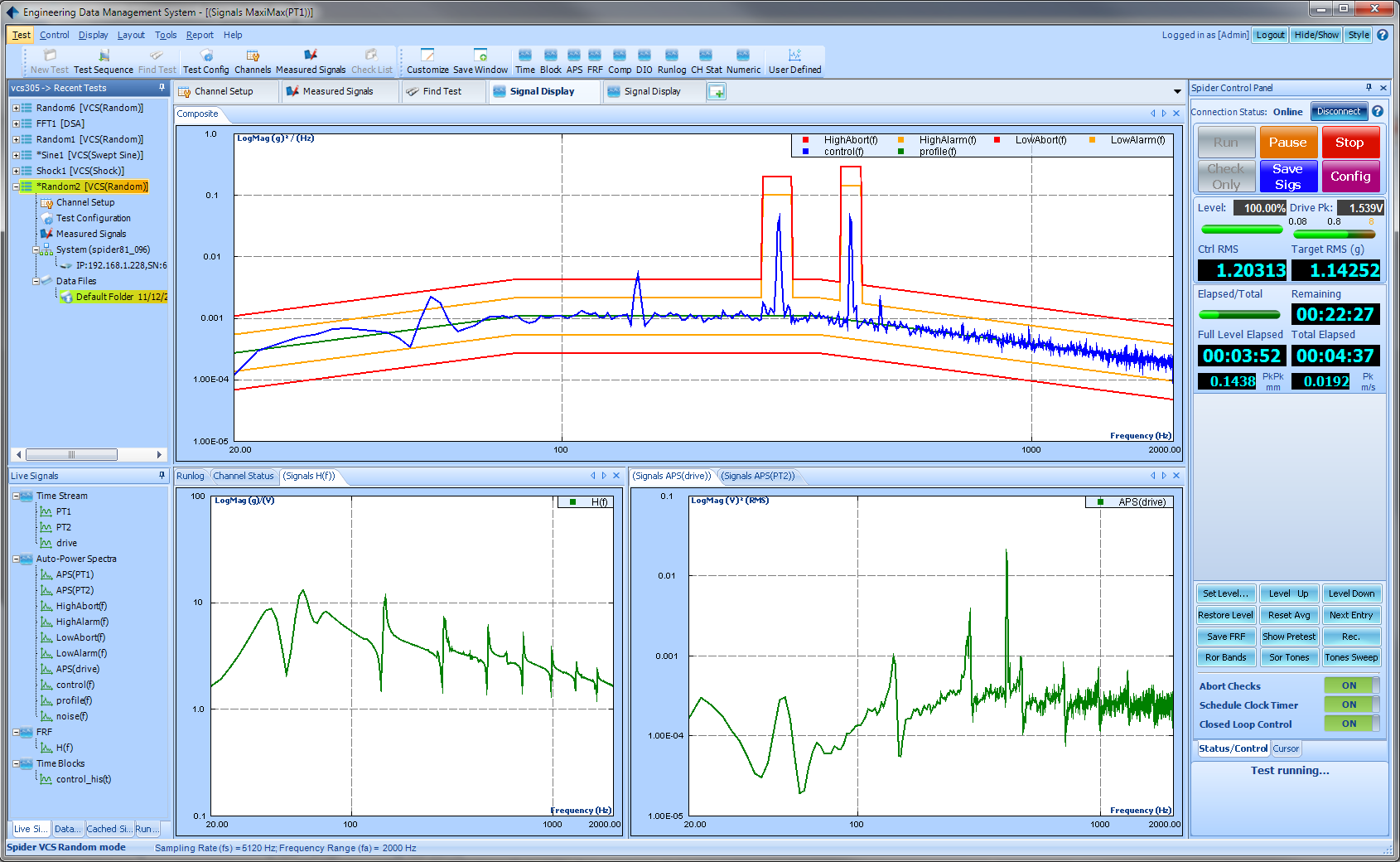
The Random Vibration Testing System provides precise, real-time, multi-channel control & analysis. Random vibration testing supports up to 512 input channels. Users can enable up to 128 channels for control and notching. Users can designate the rest of the channels as monitoring and time data recording channels.
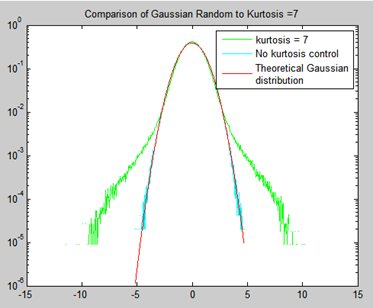
The recording option records time stream data at a full sample rate on all input channels. A unique hardware design provides a fast loop time of less than 15 ms. An optional Kurtosis control can create a non-Gaussian random signal. Annual updates are available through a convenient software subscription.
Random Vibration Testing
Control Parameters
- Frequency Range: up to 46 kHz
- Spectral Resolution: 200, 400, 800, 1,600, 3,200 and 6,400. 3,200 for all 8 channels. 25,600 optional.
- Spectral Resolution (Multi-Resolution is enabled): With Multi-Resolution enabled, equivalent resolutions of up to 25,600 lines for all 8 channels/module.
- Loop Time: 12.5 ms for 2000 Hz.
- Average Number: 1 - 500 (2 – 1000 DOFs)
- Overlap Ratio: none, 50%, 75%, and 87.5%
- Control Dynamic Range: 90 dB
- Control Accuracy: ±1 dB at 99% confidence with 200 DOF
- Drive Sigma Clipping: 3 - 10
Unique Advantages
Displacement Optimization for Random: A proprietary algorithm was developed to minimize displacement during Random Vibration Control testing. Displacement is reduced by 10% to 20% while the target PSD profile can still be reached. (Patent pending.)
Multi-resolution Function for Random Vibration Testing: EDM provides the multi-resolution feature that applies the selected resolution in the high-frequency range and 8 times of the resolution in the low-frequency range. The cutoff frequency, which divides the low and high-frequency range, is calculated by the software. (Patent pending.)
Control Dynamic Range in Random: One of the key requirements for a random controller is to achieve high control dynamic range. Control dynamic range is a measure to compare the highest and lowest spectrum amplitude in the control signal. Spider vibration controllers can achieve at least 90 dB control dynamic range. This can be measured by a modified Chinese testing standard, JJG-948. The JJG-948 only requires a control dynamic range up to 60 dB. By modifying the noise floor to lower quantity we can show much higher control dynamic range.
Safety Features
- Abort Sensitivity: a single parameter allows the sensitivity and tolerance of various safety checks to be easily adjusted between customizable lower and upper bounds
- Shaker Safety Limits: limits for shaker acceleration, velocity, and displacement
- Open Loop Detection: open loop detection for the control signal and each input channel. Detection is based on maximum control loss or maximum RMS rate of change in the input channels.
- RMS Limits: RMS limits for control signal
- Control Spectral Limits: spectral limits for control signal, starts at full level or low level
- Max Drive Limit: maximum voltage limit for drive output
- Shutdown: user-defined shutdown rate in dB per second
- Sensor Response Detection: calculation of coherence signals between input channels and drive
Continuous Data Recording
During vibration control, all measurement input and drive signals can continuously record to a Spider-NAS or the internal storage residing in each front-end. Users can view and analyze data files with Crystal Instruments Post Analyzer. The variable sampling rate can be enabled to simultaneously record slow-change signals together with high speed vibration data.
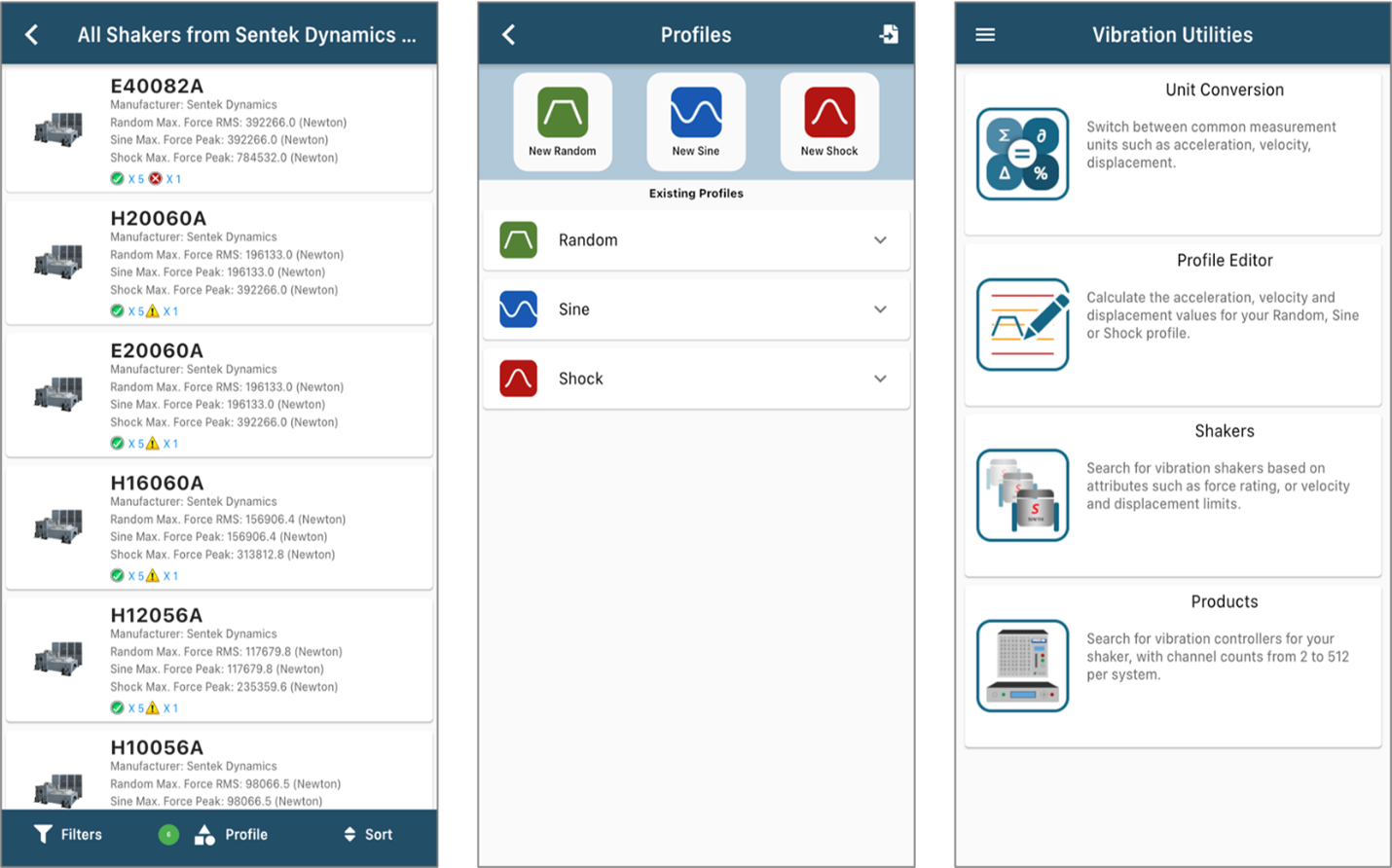
Vibration Utilities App
Crystal Instruments in partnership with our sister shaker company Sentek Dynamics provides users with the Vibration Utilities mobile app on iOS and Android. This app provides calculation features for sizing your vibration profile (Random, Sine or Shock) and searches through our catalogue of shakers and controllers for the best fit.


Random Vibration Testing Hardware
- Spider-81/81B Vibration Test Controller
- Spider-80Xi High Channel Vibration Test Controller - Scale up to 512 Channels
- Spider-80X Dynamic Measurement & Vibration Control System
- Spider-80M MIMO Vibration Test Control System
Random Vibration Testing Software Options
- Sine-on-Random Vibration Testing
- Random-on-Random Vibration Testing
- Kurtosis Control for Vibration Testing
- Fatigue Damage Spectrum in Random
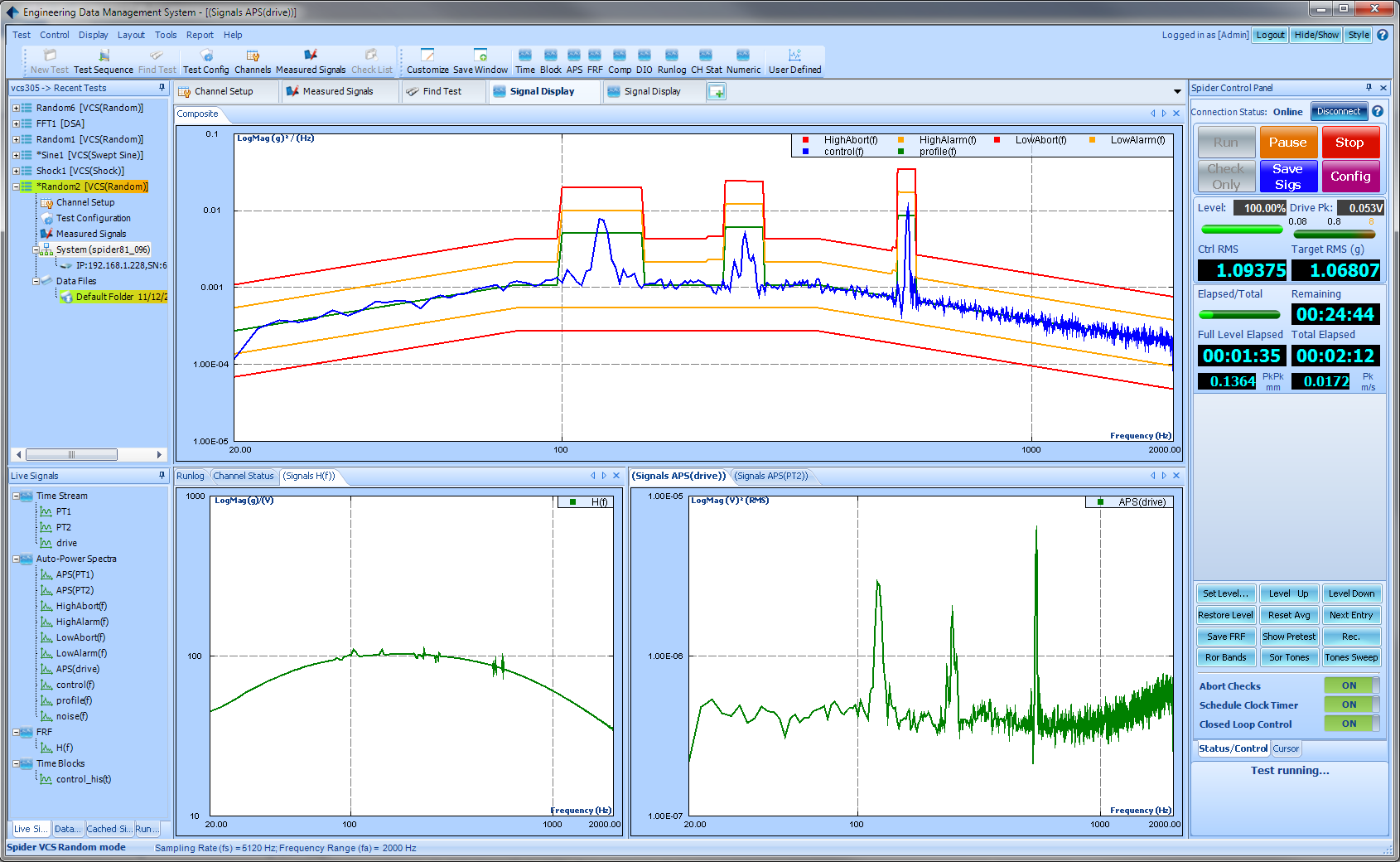
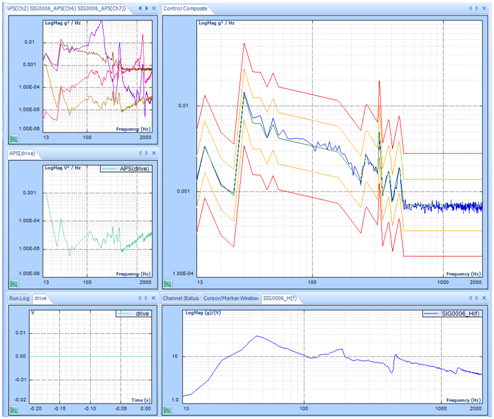
Drive Notching/Limiting for Random
Limiting is applied to control or monitor channels. Three types of limiting are available in Random Control: frequency domain, time domain, and advanced limit. Frequency domain limiting is spectrum limiting. Limit types are notching limit, abort limit, and alarm limit.
Time domain limiting compares raw data or the RMS value of input channels to the high limit. The occurrence of exceeding the high limit is one of the system events to which desirable actions can be added.
Advanced limit includes summed channel notching and vector notching. A summed virtual channel is defined as the weighted average of raw time stream signals from multiple input channels. The notch profile of a summed channel is defined in the frequency domain.
A vector RRS signal is defined as the vector sum of raw time stream signals from 3 input channels. The notch profile of a vector RRS signal is defined in the frequency domain as well.
Supports up to 128 notching/limiting channels out of 512 input channels.
Monitoring Through EDM Cloud
All vibration tests in EDM-VCS support status checks through EDM Cloud. With EDM Cloud support, users can set up any VCS test to upload live data or run logs for completed tests to a cloud storage space provided by Crystal Instruments, where data is securely stored in the user’s account.
The EDM Cloud website is located at https://cloud.go-ci.com. Users can access EDM Cloud from anywhere in the world to check the status of past and current tests. A secure login flow ensures the status can only be checked by authorized personnel with proper credentials. Multiple logins for accessing the same Cloud account is available.
|
|
|
|
|
|
|
|