Understanding the Stability Diagram
Download PDF | Jeff Zhao, Ph.D. - Senior Product Manager | © Copyright Crystal Instruments 2018, All Rights Reserved.
The Stability Diagram is an effective way to display and identify the modes of a structure under test. Nowadays, the Stability Diagram is the standard method for the modal parameter identification stage. It provides a graphical representation of the system's poles (modes) at different mode orders during the modal parameter identification stage.
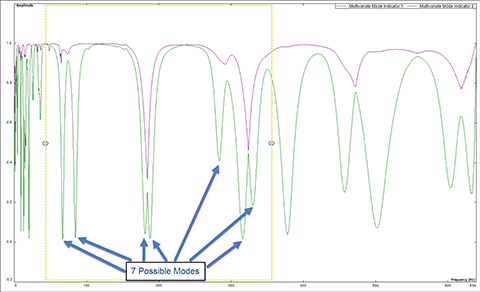
When modal analysis emerged and progressed, counting the number of peaks within a selected frequency band of the FRF signals was a typical process to begin parameter identification. The out-of-band effect can be considered by adding a few more modes (poles) to the process. From the following MMIF graph, seven modes can be counted. Then, a curve fitter will utilize the least square technique type to identify the poles. This method would still be time consuming due to time and computer performance.
Differing from the classic method above, the Stability Diagram method (which was probably put into use from the early 90’s,) will run the curve fitting process multiple times by increasing the number of poles (modes) employed. It is constructed by plotting the changes of poles in the mode order. At each mode order, the same curve fitting method is used to fit the poles. Time domain or frequency domain curve fitting methods are usually available from the modal package.
In the Stability Diagram, the physical poles (modes) of the structure under test will be identified with the same or very close values. These are the stable poles. Meanwhile, the computational poles (modes) introduced due to the increasing mode order tend to show scattering values as frequency or damping values shift all around. These poles are not stable.
All poles are labelled with different symbols based on whether they are stable. Three types of pole are plotted and labeled on the stability diagram after the iterations of the curve fitting processes. The following stability diagram displays a processed set of real data.
New pole, Stable Frequency pole and Stable pole are defined as following:
New pole: computational pole, labeled with a red circle.
Stable Frequency: pole has a stable frequency, meaning deviation of frequency is within the stable criterion, but damping deviation is higher than the stable criterion. It is illustrated with a blue diamond symbol.
Stable Pole: the pole with both frequency and damping deviations within the criteria. It is labeled with a green cross symbol. These poles can be selected as modes are identified.
Along with the MIF functions, the poles are shown with different symbols per pole order from one to the max. Hover the mouse over any pole to view its rank of mode order, Frequency, Damping, and Type will be illustrated at the bottom of the stability diagram.
From viewing the Stability Diagram above, it is easy to identify the stable poles and the physical poles. The green cross symbol poles represents a selection. At each frequency, pick one green cross labeled a stable pole. Left mouse-click on it to select that pole and add it to the Poles list on the right side of the display window. Select all the physical poles within this frequency range.
Figure 3. Stable Poles selected on Stability Diagram
The selected Pole(s) from the Poles list can be removed from the list by clicking the Delete Pole button located at the lower right corner. The user can also right-click the mouse on the stability diagram graph to select “remove cursor” from the entry.
Once all the physical poles are selected, click the Calculate Modes button to launch mode shape identification. With the mode shape data processed, the curve fitting process is completed, and the user can move on to the next mode shape animation step.