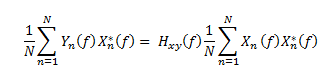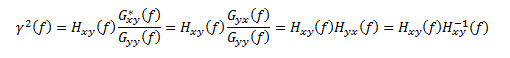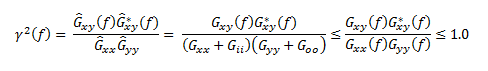The Coherence Function - A Brief Review
Download PDF | © Copyright Crystal Instruments 2016, All Rights Reserved.An important application of Dynamic Signal Analysis is characterizing the input-output behavior of physical systems. In linear systems, the output time history, y(t), can be predicted from a known input time history, x(t) if the Frequency Response Function (FRF) of the system is known.
The Fourier Transform and its inverse relate the observable time histories and their spectra. Specifically:
X(f) = F {x(t)}
and
y(t) = F-1 {Y(f)}
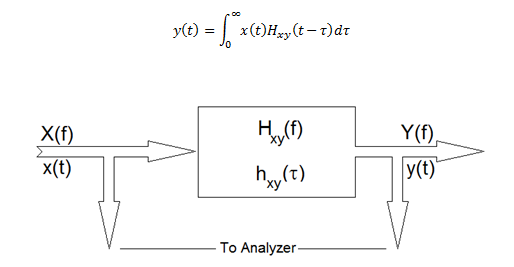
A linear process is defined by its Impulse Response, hxy(τ), or by the Fourier Transform of its Impulse Response which is called the Frequency Response Function, Hxy(f). In the time domain the system output, y(t), is predicted by the convolution of x(t) and Hxy(τ). Specifically:
This same relationship is far simpler to describe in the frequency domain. The Frequency Response Function, Hxy(f), relates the Fourier Transform of the input X(f) to the Fourier Transform of the output Y(f) by simple multiplication:
Y(f) = Hxy(f) X(f)
Multiplying both sides of this equation by the conjugate of the input spectrum and ensemble averaging explains the importance of the power and cross power spectra as they allow Hxy(f) to be directly measured. That is:
In simpler notation:
Gxy (f) = Hxy (f) Gxx (f)
...where Gxx(f) is the average auto-spectrum of X and Gxy(f) is the averaged cross spectrum between input X and output Y. From which:
Hxy(f) = Gxy(f) / Gxx(f)
The fact that Y(f) is directly dependent on the input X(f) is what makes the system linear. However, when measuring the input-output behavior of a system, there is always noise present that obscures the input and output measurements. An important measure is how much of the measured output is actually caused by the measured input and a linear process best estimated by Hxy(f). This is indicated by another important spectrum called the (ordinary) Coherence Function. This Coherence Function is also defined in terms of the cross spectrum and the power spectra. Specifically:
γ2 (f) is a real-valued spectrum. Its amplitude is dimensionless and positive and limited between 0 and 1. Note that the coherence formulation can also be stated as the product of an FRF with its inverse function. That is, if Hxy(f) measures a process going from input, x, to output, y, Hyx(f) characterizes the same process, but treats y as the input and x as the output.
This product definition indicates the coherence characterizes an "energy round trip" or a reflection through the process. We apply Gxx to Hxy and get Gxy at the output. Then we conjugate Gxy (equivalent to flipping or reflecting x(t) in time) and pass it back through Hyx. In a perfect world, this would result in exactly Gxx as the output of Hyx.
If the system is linear and none of our measurements are contaminated by noise, the round-trip is perfect and we get back everything we put in. That is, the Coherence will be exactly 1.0. If the system is non-linear or if extraneous noise has been interjected at the input or output, the round-trip will be less efficient and the Coherence will be less than one (but never more).
Thus, the coherence magnitude at every frequency is always between 0 and 1. A coherence of 1.0 means the output is perfectly explained by the input (i.e. the system is linear and the Hxy(f) measurement is perfect). A coherence of 0 means the output and input are totally unrelated. Values in-between state the fraction of measured output power explained by the measured input power and a linear process. Departures from unity can indicate input noise, output noise, a non-linear process or any combination of these things. Experienced analysts always use the Coherence measurement to quantify the quality of an FRF measurement at every frequency.
Note that ensemble averaging must be used for the Coherence to have meaning. The coherence computation for a single set of input and output "snapshots" will always evaluate to 1.0 at every frequency. This can be understood by expanding the Coherence equation to show the averaging process.
Now if we specify a single frame measurement (N=1):
Clearly then, the Coherence becomes more definitive as the number of spectra averaged increases. We will revisit this point shortly.
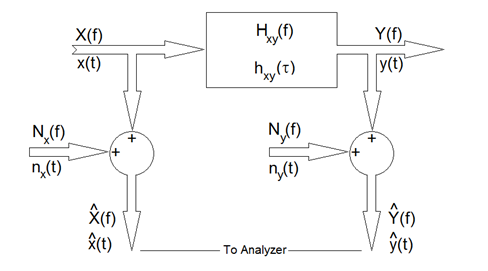
Let’s examine the effect of experiment-unrelated input and output noise on the Coherence function. As shown above, unintentional noise may be added to the input and output signals measured by our analyzer. This may be caused by a bad cable, sensor frailties or a host of other experimental “gremlins”. Further, if the process being tested exhibits some non-linear behavior, this will generate harmonics and other distortion products at the output; these appear as components of the output noise signal, o(t).
While the system on test sees an input, x(t), and produces an output, y(t), the analyzer measures the noise-contaminated signals:
The measured power spectra and the cross spectrum evaluate to:
In the (very likely) event that the input noise, i(t), is uncorrelated (unrelated) to the input stimulus, x(t), and the output noise, o(t), is completely unrelated to the system response, y(t), and i(t) and o(t) are uncorrelated, then all of cross spectra except Gxy(f) have an expected value of zero. Thus we find:
Computing the coherence from these results in:
That is, noise contamination of either signal (or equivalent output noise due to a non-linear process) causes the coherence to be reduced from that of a noise-free measurement. But, there is no way to distort or contaminate the signals that will cause γ2(f) to exceed unity.