Basics of Modal Testing and Analysis
Download PDF | © Copyright Crystal Instruments 2016, All Rights Reserved.Contents: 1. Section One | 2. Section Two | 3. Section Three
Section 1
Introduction
Modal analysis is an important tool for understanding the vibration characteristics of mechanical structures. It converts the vibration signals of excitation and responses measured on a complex structure that is difficult to perceive, into a set of modal parameters which can be straightforward to foresee. While the mathematics and physics that govern this subject are not simple, the basic concept and application can be easily understood through the examples and concepts discussed here.
This paper discusses the concept of modal analysis, its applications where modal analysis is useful, data acquisition and visualization techniques. It assumes that the reader has a basic understanding of vibration terminology and theory. For an introduction to vibration testing and analysis, refer to Crystal Instruments' "Basics of Structural Vibration Testing and Analysis".
The Modal Domain
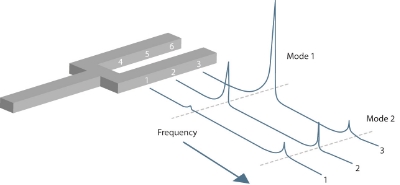
The modal domain is one perspective for understanding structural vibrations. Structures vibrate or deform in particular shapes called mode shapes when being excited at their natural frequencies. Under typical operation conditions a structure will vibrate in a complex combination which consists of all mode shapes. However, by understanding each mode shape the Engineer can then understand all the types of vibrations that are possible. Modal analysis also transfers a complex structure that is not easy to perceive, into a set of decoupled single degree of freedom systems that are simple to understand. Identification of natural frequencies, modal damping, and mode shapes of a structure based on FRF measurements is called Modal Analysis.
For example if a simply supported beam is excited at its first natural frequency, it will deform by following its first mode shape. This first mode is also called V mode as illustrated in Figure 1. The beam will move back and forth from the position shown in solid line to the position shown in dashed line. If the beam is excited at the second natural frequency the second mode shape will be excited, which is often called the S mode. If the beam is excited at a frequency between the first two natural frequencies then the deformation shape will be some combination of the two mode shapes. The third mode shape is often called the W mode. As the mode number goes higher, more node points will be observed.
Figure 1. Mode shapes of a simply supported beam
Dynamic analysis of finite element method can be used to predict the vibration characteristics of a structure under design. The structure is represented by a theoretical collection of springs and masses and then a set of matrix equations can be written that describes the whole structure. Next a mathematical algorithm is applied to the matrices to extract the natural frequencies and mode shapes of the structure. This technique is used to predict the modal parameters before a structure is manufactured to find potential issues and address them early in the design process.
After a structure or prototype is built, experimental modal analysis can be applied to determine the actual modal parameters of the structure. Experimental modal analysis consists of exciting the structure in some way and measuring the frequency response function at all meshing points on the structure. For example the tuning fork shown in Figure 2 is a very simple structure. The FRFs could be measured at various points producing the results shown in Figure 2. The natural frequencies are indicated by the peaks that appear at the same frequency at every point on the structure. The amplitude of the peak at each location describes the mode shape for the associated resonant frequency. The damping of each mode is indicated by the sharpness of each peak.
Figure 2. Modal analysis of a tuning fork
The results shown indicate that for the first mode, the base of tuning fork is fixed and the end experiences maximum deformation as shown in Figure 3. The second mode has maximum deflection at the middle of the fork as shown in Figure 3.
Figure 3. The first mode shape and the second mode shape of the tuning fork
Applications for Modal Analysis
The mode shapes and natural frequencies, called the modal parameters for short, of a structure can be predicted using mathematical models known as Finite Element Analysis (FEA) models. These discrete points that are connected by elements with the mathematical properties of the structure’s materials. Boundary conditions are applied that define how the structure is fixed to the ground or supported, as well as the loads applied. Once the model is defined, a mathematical algorithm is applied and the mode shapes and natural frequencies are computed. This data helps Engineers design structures and understand the vibration characteristics before the structure is even built. Figure 4 illustrates a FEA model of a space vehicle with force loads and boundary conditions.
Figure 4. Finite Element Model of a space vehicle.
Once the structure is built, it is a good practice to verify the FEA model using Experimental Modal Analysis (EMA) results. This correlation analysis between the EMA and FEA results identifies errors in the FEA model and helps to update the FEA model. Experimental Modal Analysis can also be carried out without FEA models, simply to identify the modal parameters of an existing structure to understand the vibration characteristics of the structure.
Modal analysis is an important tool for identifying and solving structural vibration related issues. One common vibration issue that can be identified with modal analysis occurs when an excitation function interacts with the natural frequency of the structure. Any excitation will cause the structure to vibrate, from the rotational imbalance in an automobile engine, or reciprocating motion in a machine, or broad band noise from wind or road noise in a vehicle. The excitation function can be analyzed in the frequency domain to determine its frequency components. When the frequency of the excitation coincides with a natural frequency of the structure, the structure may exhibit very high level of vibrations that can lead to structure fatigue and failure.
Modal analysis identifies the natural frequencies, damping coefficients, and mode shapes of the structure. When it is known that the excitation force coincides with one of the natural frequencies found in the modal analysis, the structure can be redesigned or modified to shift the natural frequency away from the excitation frequency. Structural elements can be added so as to increase the stiffness of the structure or mass can be increased or decreased. By doing that, the excitation frequency will no longer fall on the natural frequency of the structure. These techniques can be applied to move the natural frequencies away from the excitation force frequency. Other techniques of vibration suppression include increasing the damping of the structure by changing the material or adding viscoelastic material to the surface of the structure. Vibration absorbers can be added which are tuned to the excitation force frequency to yield large vibrations in the absorber and reduce the vibration in the structure.
Figure 5. Vibration isolators (left) and absorbers (right) are methods of passive vibration suppression.
When these techniques do not work well, active vibration controls can be applied which measure the vibrations and use a computer to generate a drive signal that drives an actuator to counteract the vibrations in the structure.
Figure 6. Damping treatment is the most common and active suppression is the most expensive technique for vibration
For all these vibration treatment techniques, modal analysis is usually the starting point to understand the natural frequencies, damping and mode shapes of the structure. The modal parameters help to identify the issue and lead to an effective solution.
Section 2
Modal Data Acquisition
The first step in experimental modal analysis is to measure the excitation and responses of the structure under test. The structure must be excited and the applied excitation force and resulting response vibrations, typically accelerations, are both measured resulting in a Frequency Response Function data set. The FRF data set can be used to identify the modal parameters, including natural frequencies, damping coefficients, and mode shapes. The mode shaper data can be then animated visually.
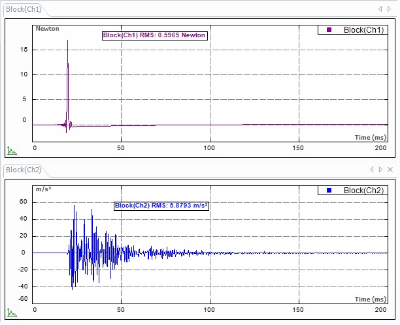
The structure must be excited to have the vibrating responses. There are two common methods of excitation: impact hammer and modal shaker. An impact hammer shown in Figure 7 is a specialized measurement tool that produces short duration of excitation levels by striking the structure at certain point shown in Figure 8. The hammer is instrumented with a force sensor which generates a voltage signal proportional to excitation force so that the excitation force is measured during the test. Impact hammer is often used for modal analysis on simple structures, or where attaching a modal shaker is not practical. Different hardness impact tips can be used with the hammer to change the measurement frequency range of the impact. When low frequency measurements are needed, a soft rubber tip may be used, and when high frequency measurements are needed, a hard metal tip may be used.
Figure 7. Impact hammer instrumented with a force sensor with different hardness tips.
Figure 8. Impact hammer force versus time (input1) and structural response versus time (input2)
For laboratory modal testing measurements, a modal shaker is often used. Modal shakers are rated by the force they can produce and vary in size. Typically modal shaker systems are rated from several lbfs to 100 lbfs of sine force. The selection of modal shaker size is based on the driving forces required so as to get enough level of responses on the structure under test.
Figure 9. Modal Shakers are used in laboratory measurements and vary in size
Typically, a modal shaker is connected to the structure with a small thin metal rod called “stinger”. A force sensor is placed on the structure at the driving point, and connected to one end of the stinger, to measure the excitation force. Quite often, an accelerometer is also mounted on the structure at the driving point to measure the acceleration levels. And this can be easily done by applying an Impedance head (force and acceleration sensor in one to the driving point on the structure).
A shaker is often driven by the dynamic signal analyzer’s DAC (digital to analog converter), which is an electronic device to generates carefully tuned electronic signals which are then amplified and converted into the excitation signals. There are several different types of excitation signal profiles can be used to excite the structure, including pure random (white noise), burst random, pseudo random, periodic random, chirp (burst chirp), etc.
A random profile creates a random type of excitation which includes a broad range of frequencies. Windowing and averaging can be applied to the data acquisition when random vibration is used. One advantage of random vibration is that the profile can be programmed so that energy is distributed across all frequencies to get the optimal vibration measurements. Following Figure illustrates random excitation and acceleration response signals from a modal testing.
Figure 10-1. Random excitation and response signals used by a modal shaker to excite structure for modal testing
Burst random consists of a portion time with a random vibration, followed by a portion time with no excitation. The on/off period can be programmed so that the vibrations of the structure dissipate at the end of the off period. This has the advantage that no windowing is required because the excitation and response are both periodic. Burst random excitation yields much more accurate amplitude and damping measurements compared to a random excitation.
The pseudo random is an ergodic, stationary random signal consisting of energy content only at integer multiples of the FFT frequency increment (Δf). The frequency spectrum of this signal has a unity shape which has a constant amplitude along the frequency axis, but with randomized phase. While the periodic random signal is also an ergodic, stationary random signal consisting only of integer multiples of the FFT frequency increment. The frequency spectrum of this signal has both randomized amplitude and randomized phase distribution.
With above two types of random signal, if sufficient delay time is allowed in the measurement procedure for any transient response to the initiation of the signal to decay (number of delay blocks), the resultant input and output histories are periodic with respect to the sample period. For one spectral average the time signal derived from the above frequency spectrum is repeated (Nd + Nc) times. The first Nd are there to allow periodic response of the structure; the Nc following are measured and cyclically averaged (time average). The effect of using these two types of random, is that a better ‘linear equivalent’ of the structure is obtained at the cost of much longer testing time.
Chirp signal is a short profile that consists of a sine tone starting at a low frequency and quickly sweeping to a high frequency usually in a time of a second or less. After one sweep there can be a quiet period, and the chirp signal repeats over and over. The quiet period is programmable to a length to allow the structural responses to damp out before the end of each time frame. This ensures that the excitation and response are periodic within each time block. It has the advantage of that it excites all frequencies and is periodic so that no windowing is required, as long as the signal analyzer sampling time is synchronized with the chirp signal. It also has a better signal to noise ratio compared to random excitation measurements. A typical Burst Chirp excitation and Response signals are illustrated in Figure 10-2.
Figure 10-2. Burst Chirp excitation and response signals used by a modal shaker to excite structure for modal testing
Measurements: FRFs, Coherence, APS
Once the structure is excited, the next is to measure the excitation as well as the response(s). This is normally done by placing force sensor and accelerometers on the structure and measuring/recording the force and acceleration responses with a Dynamic Signal Analyzer. An accelerometer is an electronic sensor that converts electronic signal into acceleration and measures it. There are uniaxial and tri-axial accelerometers available. A tri-axial accelerometer is in fact three accelerometers in one, which are aligned perpendicular to each other, thus to provide the vibration measurement along all 3 axes. A Dynamic Signal Analyzer is an instrument that measures and records the signals and computes these signals into frequency domain data.
An important consideration for modal data acquisition is the number of measurement points needed for the structure. Too many points will result in an unnecessarily large data set and wasted time. Too few points will result in a poor representation of the structure and may not capture the desired mode shapes. Some engineering judgment must be used to estimate the likely mode shapes and then choose a number of points that can accurately represent the structure.
The most common types of signals that are used in modal analysis are Frequency Response Functions (FRFs) and Coherence. From the linear spectrums, Auto Power Spectrum, Cross Power Spectrum can be computed. And averaging of multiple FFT results is involved so as to reduce the noise effect. The H1 type of FRF estimation can be calculated from the Gyx vs Gxx.
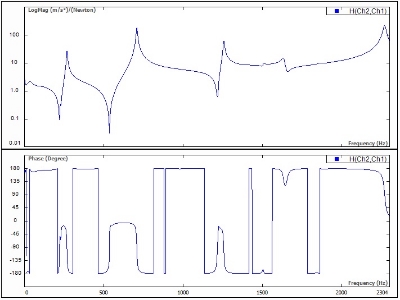
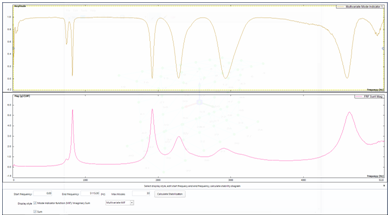
Frequency Response Function (FRF) is computed from two signals, namely response (output) and excitation (input). It is sometimes called a “transfer function”. The FRF describes the ratio of one signal with respect to another signal over frequency range interested. It is used in modal analysis where the acceleration response of the structure is measured relative to the force excitation from the impact hammer or modal shaker. An FRF signal measured is a complex signal with either Magnitude/Phase, or Real/Imaginary information. Figure 11 illustrates a typical FRF in Bode Diagram with Magnitude and Phase presentation.
Figure 11. Frequency response function with magnitude (top) and phase (bottom).
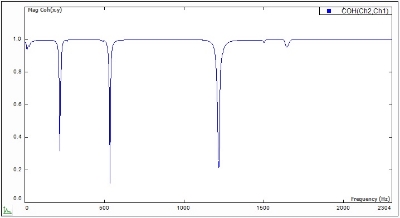
Coherence is related to the FRF and tells what portion of the response is attributed to the excitation. It is a function of frequency that can vary from zero to one. In modal analysis this signal is used to assess the quality of a measurement. A good excitation produces a vibration response that is perfectly correlated to the excitation force, indicated by a coherence graph that is close to one over the entire frequency range. Coherence should be monitored during data acquisition to ensure that the data is valid. The coherence overall should be close to 1 across the frequency range. However, it is normal for coherence to be low at an anti-resonances, or structural nodes where the vibration responses are very low as shown in Figure 12.
Figure 12. Coherence function shows the quality of the FRF data.
Averaging
Frequency domain data is normally computed from one block of time data. Every block of time data includes some random noise that can obscure the true resonant frequencies and mode shapes. By averaging several blocks of data, the uncorrelated random noise will be reduced. Note instrument noise is not affected by averaging. Signals can be averaged using a linear average where all data blocks have the same weight, or they can be averaged using exponential weighting so that the last data block has the most weight and the first has the least. Averaging has the advantage of reducing the effect of random noise and resulting in smoother data. Generally speaking, frequency domain averaging does not eliminate background noise but it does a better estimate of the mean value for each frequency point.
For example, Figure 13 illustrates the effect of averaging on a random signal. The top pane shows the spectrum with only one frame, the middle pane shows the spectrum after 10 averages and the bottom pane is after 40 averages. The variations from one frequency line to the next are smoothed out as more number of averages are involved.
Figure 13. Averaging reduces the effect of uncorrelated random noise resulting in smoother averaged spectra.
The Engineer must use judgment to determine the number of averages to use in every application. User needs to consider the randomness of the signal under measurement, the quality of the results required and the length of time needed for each frame acquisition. In general a rule of thumb is to use 32-64 averages for shaker testing, while 4 to 8 averages for hammer impact testing.
Section 3
Triggering
Triggering is a technique for having the analyzer wait to start capturing data until an event occurs such as an impact hammer “bangs”. A trigger can be set up so that the data acquisition and processing will not start until some voltage level is detected in an input channel. After the trigger is armed, the analyzer will be initialized and wait for the impact to occur and start acquiring of data by then. Triggering can be set up so as to automatically re-arm after each trigger so that several hammer impacts can be performed one after the other and averaged without the need of interacting with the signal analyzer. Care must be taken so that the start of the data before the triggering point is not excluded, and this can be done through the negative pre-trigger setting. A pre-trigger can be set so that some data points are captured immediately before the trigger is activated. This ensures that the entire impact waveform is captured in one time frame.
Figure 14. Software interface for trigger setup.
For modal shaker case, the so called source trigger type is employed to have the data acquisition aligned with the source output. This is critical, especially for the burst type of excitation signals and periodic random signals, i.e., burst random, or pseudo random. The idea is to include all the signals inside one frame, and maintain the periodic characteristics of these signals.
Windowing
Windowing is a technique that is necessary when computing FFTs while measured signal is not periodic in the time block. It is in general needed when a shaker is used to excite the system with broadband random noise. When the FFT of a non periodic signal is computed the FFT suffers from what is known as leakage phenomenon. Leakage is the effect of the signal energy smearing out over a wide frequency range when it would be in a narrow frequency range if the signal were periodic. Since majority of signals are not periodic in the data block time period, windowing would be applied so as to force them to be periodic, and alleviate the leakage.
A windowing function is shaped so that it is exactly zero at the beginning and end of the data block and has some special shape in between depends on the windowing type. This function is then multiplied with the time data block forcing the signal to be periodic. A special window function weighting factor must also be applied so that the correct FFT signal level is recovered after the windowing. Figure 15 illustrates the effect of applying a Flattop window to a pure sine tone. The left top graph is a sine tone that is perfectly periodic in the time window, and no windowing is applied. The FFT of this sine tone (left-bottom) shows no leakage, that is, the FFT spectrum is narrow and has peak magnitude of one which represents the magnitude of the sine wave in time domain. The middle-top plot shows a sine tone that is not periodic within the time window resulting in leakage in the FFT in frequency domain (middle-bottom). The leakage reduces the height of the peak and widens the base. When the Hanning window is applied (top-right), the leakage is reduced in the FFT signal (bottom-right), and the magnitude is corrected, though the width of the peak is still widened.
Figure 15. Hanning window (right) reduces the effect of leakage (middle)
Leakage is easy to understand with pure sine tones, however it also affects measurements with all other types of waveforms. Figure 16 shows a frequency response function with and without a window (Hanning Window). Here the energy smearing effect of leakage is most evident in regions where there is a deep valley. Leakage can also affect the amplitude and thus frequency readings the same way as with sine waveforms.
Figure 16. Frequency response function with and without window.
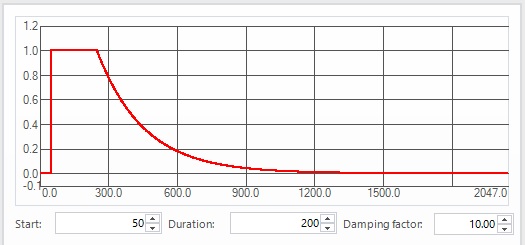
When an impact hammer is used to excite the structure the time block length can be adjusted so that the measured response totally dissipates within the time block. In this case since the signal starts at zero and ends at zero no windowing is required, and this will yield the most accurate amplitude and damping results. When a lightly damped structure continues to ring for a very long period of time, or when some background noise is present, a special windowing function called force/exponential window can be used. This window function, shown in Figure 17, has two parts, the force window at the beginning of the time frame, and the exponential window followed till the end. The force window includes a hold off period that eliminates any instrumentation noise before the impact. The length of this hold off period can be specified by the user to coincide with the pre-trigger time reducing the effects of noise. The exponential window followed till the end of the time frame applies an exponential decay that forces the vibration response of the structure to zero by the end of the frame resulting in a guaranteed periodic signal. It should be noted that this will result in an over-estimate of the damping of the structure because this windowing function artificially adds damping to the signals in a shorter time.
Figure 17. Force/exponential window function is used for modal analysis with impact hammer excitation.
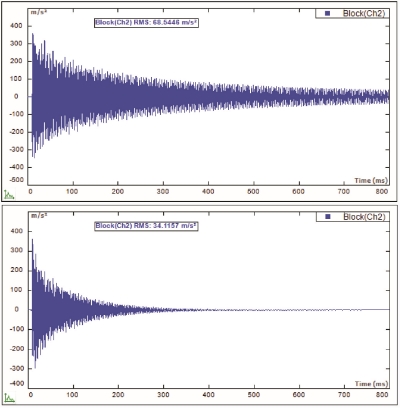
Figure 18 shows the time response of a structure without the window in the top frame. Note that the vibration has not died out at the end of the time record. The bottom frame shows the results of adding the force/exponential window. The vibrations are forced to zero at the end of the time record by the window.
Figure 18. Time response of lightly damped structure without (top) and with exponential window (bottom).
Enhancing Measurement Resolution
One important consideration in modal testing measurements is the frequency resolution, or distance between frequency lines. When natural frequencies occur close together, a finer frequency resolution may be needed to accurately represent the frequency and damping of the two peaks. There are two ways to increase the frequency resolution: increasing frame size, or using FFT zoom analysis. The frequency resolution is determined by the number of points in the time frame, more points in the time block results in more frequency lines in the frequency domain spectrum. Thus the frequency resolution can be increased by increasing the number of points in the time block. The drawback is that a longer time frame requires more time of data acquiring, which increases the overall measurement time. This is even more noticeable when the frequency span is low, such as below 50 Hz.
The second method for increasing frequency resolution is to use FFT zoom analysis. This technique uses a special algorithm to compute the spectrum within a band that does not start from frequency zero (or DC), unlike standard “base band” spectra that are normally used when FFT zoom is not used. The dynamic signal analyzer has a setting for the center frequency, number of frequency lines and the span. Then the frequency lines are distributed between the low and high frequencies covering the frequency span, centered at the center frequency specified. The result FFR spectrum is of very fine frequency resolution compared to the standard FFT analysis.
Figure 19 shows a comparison of a frequency response function of a structure with different frequency resolutions. The first measurement is made with 400 frequency lines. The broad hump near 90 Hz is likely a pair of highly coupled modes. Due to the closely coupled nature of these two modes, the amplitude and damping cannot be accurately determined with this low frequency resolution measurement. The second measurement is carried out with the number of frequency lines increased to 1600. Now the closely spaced peaks are clearly be measured. The third measurement uses FFT zoom with a span of 300 Hz and a center frequency of 200 Hz. This gives the finest frequency resolution of all 3 measurements. Note that the FFT zoom spectrum does not show any data below 50 Hz, or beyond 350 Hz, because it is not a base band spectrum.
Figure 19. Comparison of a spectrum made with 400 and 1600 lines and with FFT zoom, illustrating enhanced measurement resolution.
Signal Quality - Overload and Double Hit
Signal quality is an important consideration in modal data acquisition. If the quality of the data is not monitored during the acquisition, the modal analysis results can be erroneous or invalid. Monitoring the coherence function is the first step in assessing the signal quality. When the coherence function is poor the steps should be taken to improve it before the final data is collected.
Other issues that affect signal quality are overload and impact hammer double hit. An overload occurs when the signal from the accelerometer or impact hammer exceeds the voltage range of the input channel on the dynamic signal analyzer. For example if input channel voltage range is set to 1.0 volts max on the analyzer, and a strong impact generates a voltage signal of 1.5 volts from the impact hammer, the input channel will overload. Most signal analyzers provide an alarm to indicate that an overload has occurred. The resulting data from an overloaded signal are completely invalid and should be discarded. The test will be repeated to retake the data. An overload can be avoided by reducing the impact forcehitting the structure more softly, by increasing the input channel voltage range on the analyzer, or by using an accelerometer or impact hammer with lower sensitivity. Most dynamic signal analyzer can detect an overload, warn the user and have the choice to discard invalid data so that it does not affect the averaged signals.
With hammer impact test, double hit occurs when the hammer hits the structure and structure rebounds into the hammer tip. The second impact may only be milliseconds after the first and easy to miss on the data display. A double hit will also produce invalid data and should be discarded and the test needs to be repeated. Double hit can be detected by viewing a time trace of the impact hammer force time history with zoom display feature during the data acquisition.
Figure 20. An impact hammer double hit can be seen in the force versus time plot and degrades the quality of the modal analysis results.
Building the Geometry Model
The geometric model of the structure can be built before modal data acquisition. The geometry model consists of points, lines, and surfaces in an arrangement to represent the shape of the structure under test. Most modal analysis software includes tools to generate these geometry elements, and typically a library of components: i.e., beam, plate, cube, cylinder, or sphere. Using the tool, any structure under test can be modeled into a geometry model. The simple elements or components can be combined to form a very complicated structure. The model can be very simple or very complex depending on the level of precision needed from the results. For example, a beam can be represented by only several points connected by lines, and it is sufficient to visualize the first few mode shapes. A complicated structure such as an engine block would need many more points and other elements to accurately represent the structure.
Figure 21. Geometry model of an I-Beam structure
The number of modes must be taken into account when the geometry model is built. Mode shapes associated with lower natural frequency modes tend to have simple mode shapes that can be readily visualized with only a few points. Modes related to higher resonant frequencies can have more complex mode shapes and the model may require finer resolution with more points to accurately represent the mode shape.
Data Labeling and Auto-Incrementing
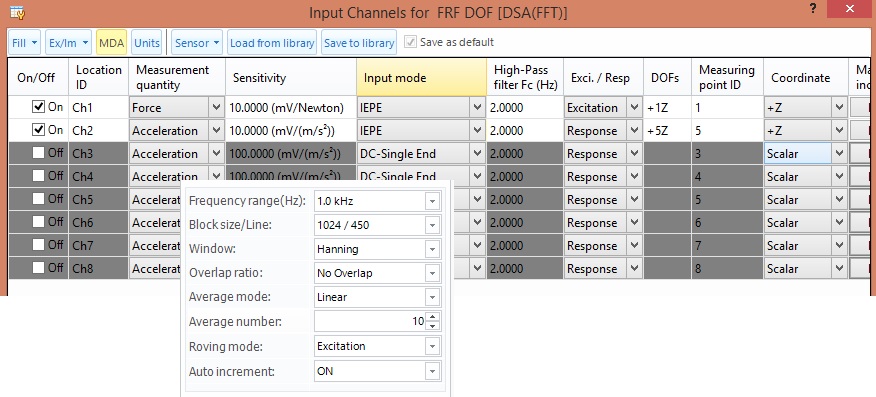
Modal data acquisition for modal analysis requires measuring the vibration response at all points on the structure. This usually results in a very large data set. Once the data is acquired it will be fed into the modal analysis stage and each measurement signal will be associated to the point and direction on the structure mesh model. The label includes so-called DOF information consisting of the point number and direction of the measurement sensor. Direction is recorded with respect to certain coordinate systems, i.e., Cartesian with +x, +y, +z, -x, -y, or -z. This DOF information can then be used by the modal analysis software to automatically assign the measurement data to the corresponding point on the structure.
Auto-incrementing is a feature that automatically increments the point and/or direction, after each measurement is complete. The DOF information can always be manually entered, or corrected during the test. Once all the required measurement DOFs are covered, the complete set of data can be saved and fed to the modal analysis software to perform the next step of analysis.
Figure 22. Modal coordinates can be automatically incremented with software.
The number of modes must be taken into account when the geometry model is built. Mode shapes associated with lower natural frequency modes tend to have simple mode shapes that can be readily visualized with only a few points. Modes related to higher resonant frequencies can have more complex mode shapes and the model may require finer resolution with more points to accurately represent the mode shape.
Assigning the Measured Data
The next step is to assign the measured data to the geometrical model. The model consists of points that are connected by lines, then possibly surfaces. The vibration response of the structure has been measured at these points represented on the model. The measured data are associated with the points on the structure in the right direction. Modal analysis software includes a tool for assigning the FRF data to points on the structure. This can be done manually by selecting points/directions on the structure, or automatically using the DOF labels from the FRF measurement data.
The data labeling and auto incrementing feature of dynamic signal analyzer will simplify this process. Typically the geometry model is created such that all points on the model correspond to the measurement points on the structure. Most software can then automatically read the data labels and apply the DOF data to the correct point numbers with the correct directions.
For some cases, not every point/direction on the structure have a measured FRF. The modal analysis software can interpolate between measured points/directions to have the FRF of the unmeasured point. For example, a beam may have 6 measured FRF points along z direction, while geometry model may have 10 points, with one extra point between every measurement point. The software will then compute the data of the interpolated points by analyzing the nearby measured points. This results in a model which looks smoother.
Identifying the Modal Parameters
The key step in the modal analysis is to identify the modal parameters of the structure. This can be carried with simple method if the structure has only a few resonance frequencies which are separated by a large frequency band, or it may require more advanced method if there are several natural frequencies that are close or repeated in the frequency response function spectrum. The damping of each natural frequency is another parameter of interest, and it is related to the sharpness of the resonance peak.
All modal analysis software includes many tools for identifying the natural frequencies and damping from the measured FRF data. These tools use different methods, SDOF or MDOF, from time domain to frequency domain, covering single reference to multiple reference. One simple SDOF method is called quaderature picking which analyzes the imaginary part of the FRF data to locate a peak. At natural frequency, the imaginary part of the FRF will normally appear as a peak, if the FRF is of the unit acceleration vs force. The mode is indicated by a positive or negative peak as shown in Figure 23.
Figure 23. Multivariate MIF and FRF SUM from a Beam.
A stability diagram is employed for modal parameter identification. The physical poles are stable and can be selected for the next step mode shape calculation. With the natural frequencies and damping coefficients identified, the software will perform one more curve fitting step to extract the residues (mode shape information) from the whole set of FRF measurement data. The mode shape is determined by identifying the amplitude and phase of the FRF at the natural frequency for every DOF (point and direction) on the structure.
Figure 24. Stability Diagram of curve fitting
The mode shape table can be saved and used for the next step of mode shape animation. MAC function and FRF synthesis are available, which provides the means of modal parameter validation.
Interpreting the Results
The final step is to interpret the results. The geometry model can now be used to run the mode shape animation. Each identified mode, with its natural frequency, damping, and mode shape, can be selected for mode shape animation. With mode shape animation, the geometry model first starts in the un-deformed position, and then deforms per a defined step, till it reaches the peak of deformation, and steps back to un-deformed position, keeps deform towards the negative side of the deformation, ... And this process cycles. The magnitude of mode shape animation can be increased or decreased to highlight the mode shape. In the meantime, the geometry model can also be rotating while it is animating the mode shape so that the mode shape can be viewed from the best perspective angle.
There are also many graphical tools can be used to help in visualizing the mode shape. Colormap which indicates the magnitude of the modal deformation with different colors is one example. Vectors of arrows can be used from the un-deformed position to the deformed position of the geometry model. All these tools are intended to give the user the ability to understand the deformation nature of each mode.
Case Study
The following case study presents the complete data acquisition and modal analysis for an I-Beam. The structure is suspended on a frame using bungee cords so as to have the free-free boundary condition. Measurement points are arranged per the geometry model built in the Geometry editor.
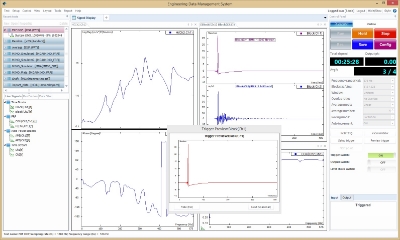
The FRF data is acquired using an impact hammer and accelerometer. The accelerometer is attached to one measurement location using wax, while the impact hammer is roving from point to point for each FRF measurement. A Crystal Instruments Dynamic Signal Analyzer with EDM Modal software is used to acquire the measurement data and modal analysis. A few test measurements determine the bandwidth, blocksize, trigger settings, windowing or not, etc. Linear Averaging with a number of 4 is set, using an input channel trigger with a pre-trigger was set to capture the pulses.
The EDM Modal software interface is set up to show the measured FRF, coherence and force and acceleration versus time. These displays are used to monitor the quality of the data during acquisition. The modal coordinate window displays the current measuring point ID number and axis while updating the point numbers with the auto-incrementing feature. The Channel Status bar indictor display can show the voltage level of input channels and indicate whether an overload occurs.
When all setups are confirmed, the FRF data can be acquired. Four hammer impacts are averaged at each measuring point on the structure. The resulting 63 FRF signals are measured and saved into the modal data selection stage.
Figure 25. Crystal Instruments Modal Analysis and Test software interface
A geometric model is constructed using the geometry editor tool, as shown in Figure 26. The geometry is following the actual structure. This geometry model is built through the definition of points, lines, and then surfaces. It includes the measure of the structure and represents the real structure. It helps not only the assignment of measurement points, but can also be used formode shape visualization, called animation.
Figure 26. Geometric model of the I-Beam
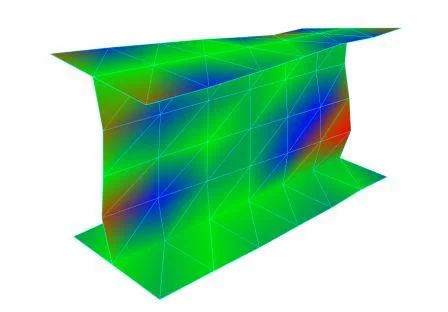
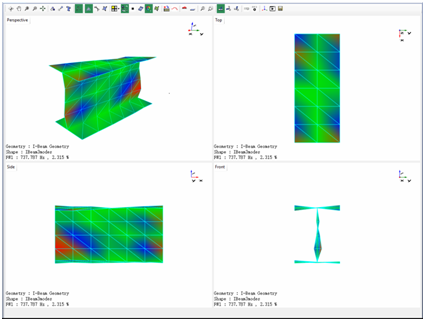
The curve fitting tools are used to identify the modal parameters, including natural frequencies, damping coefficients, and mode shapes. The first mode is shown in Figure 27. The side view in the lower left illustrates the best view of the deformation of the vertical plate. It is similar to the torsional deformation. The perspective view, along with the Top, Front and Side view illustrates the mode well by showing the node lines together with the high deformation region.
Figure 27. First mode shape with deformed colormap.
These results could be used to identify critical points on the structure that are likely to experience high levels of vibration. The mode shape gives a relatively scaled data. With the linear assumption, vibration amplitudes are proportional to the excitation levels. The structure could be modified by changing the cross-section properties, adding stiffeners or damping materials, so that the modal parameters can be changed if needed. The modal data could also be used to consider changing the mounting points of the muffler to the vehicle, for example. In many cases this type of analysis starts with a simple model to identify the areas of concern. Afterwards a refined model with detailed measurements can be produced if the time and effort are justified.
Conclusions
Modal analysis is widely used for solving vibration problems that identify the modal parameters, natural frequencies, damping, and mode shapes of the structure under testing. Simulation software, i.e., FEA, uses a mathematical model of the structure, while experimental modal analysis uses data which is measured from a physical structure. Experimental modal analysis can be carried out in two step processes. The first step consists of data acquisition of frequency response functions. The second step consists of modal parameter identification and visualization using a geometry model of the structure. The modal frequencies, damping coefficients, and mode shapes identified, can be used for the structure modification for vibration suppression, or driving function modification to avoid the resonance situation. For more detailed explanation with mathematical derivations, the following references can be referred to.
References
Inman, Daniel J., “Engineering Vibrations, Second Edition,” Prentice Hall, New Jersey, 2001.